小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題プリント 小学4年生の算数 図形 練習問題プリント 小学5年生の算数 図形 練習問題プリント 小学6年生の算数 公式をおぼえたいときに参考にしてみてね^^ 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず!体積 = 底面積 × 高さ
U9j580gf8iba369ji2w Xyz P 296
図形 面積 公式 高校
図形 面積 公式 高校-正方形の面積 一辺 いっぺん ×一辺 いっぺん =面積 めんせき a×a=a2 三角形の面積 底辺×高さ÷2=面積 a×h 2 1 a h 台形の面積 (上底下底)×高さ÷2=面積 (ab )×h 2 1 h(ab ) 平行四辺形の面積11 内接円を利用した三角形の面積 B (三角形の面積)=(abc)×r× 1 2 12 平行線と比例 A ABBC=STTU=PQQR 13 外接円を利用した三角形の面積公式 D (三角形の面積)= × × 4𝑅




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
① 面積の公式を知っている図形を見いだす。 ② 図形の面積を求め,求め方を説明する。 ーcm ーcm 下の形の面積を求めましょう。 下底 高さ 「図形と式とを関連付け,説明しよう」 ~図形の構成についての見方を働かせ,面積を求める~ 算数 TYPE S 男 女 男 小学算数角度と面積の公式 学習ポスター&クイズテスト 無料ダウンロード いろいろな形(三角形、四角形、多角形、円など)、角度、面積の公式について学べる学習ポスター&確認クイズテストです。 平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷2 台形の面積= (上底+下底)×高さ÷2 三角形の面積=底辺×高さ÷2 円の面積=半径×半径×円周率 (314) おうぎ形の面積=半径×半径×円周率×中心角/360° 公式の成り立ちから知りたい人や公式がまだ曖昧な人は こちらの記事 を読んでから、これから解説する問題に取り組んでください。 中学受験 算数
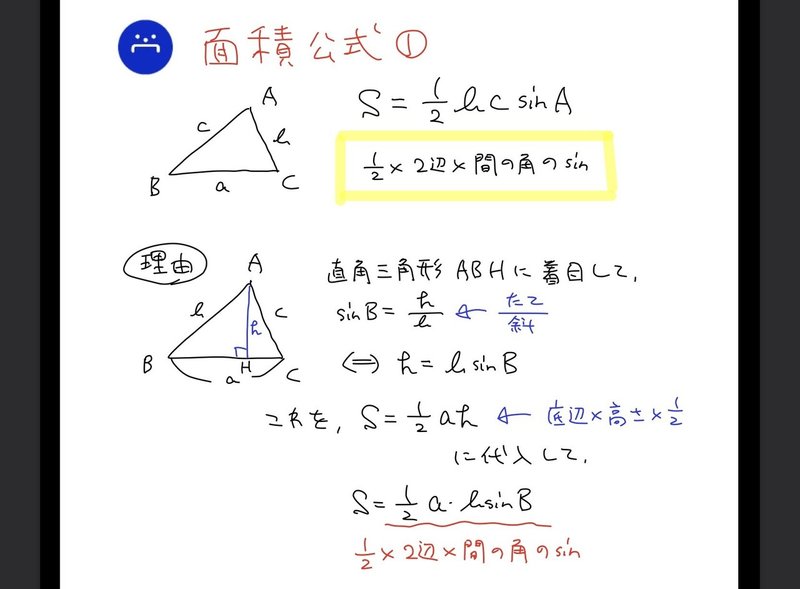
底辺の長さ $a$、高さ $h$ の平行四辺形の面積 $S$ は、次の公式で求められます。 平行四辺形 (へいこうしへんけい) の面積 \begin{align*} S = ah \end{align*} 面積 = 底辺 × 高さ 公式の 導出 (どうしゅつ) 方法と計算 例 (れい) は「平行四辺形の面積の求め方」をご覧ください。 ADE ADE = A B ⋅ A C ⋅ sin ∠ A A D ⋅ A E ⋅ sin ∠ A = A B ⋅ A C A D ⋅ A E =AB\cdot AC\cdot \sin\angle AAD\cdot AE\cdot \sin\angle A\\=AB\cdot ACAD\cdot AE = AB ⋅ AC ⋅ sin∠A AD ⋅AE ⋅sin∠A = AB ⋅ AC AD ⋅ AE図形の基本公式目次 1 角度の公式 2 長さの公式 3 面積の公式 4 等積図形・一覧
立方体 = 一辺 × 一辺 × 一辺 直方体 = 縦 × 横 × 高さ 柱体 = 底面積 × 高さ 3最近、任意の多角形に対して常に成り立つ求積公式を知ることができたので紹介したい。 たとえば、皆さんは下記の図形の面積はどのようにして求めるだろうか? 多分、多くの方は左図の図形を含む 長方形を考えて、その面積から余計な図形の「公式」が覚えられません。 中学生から、こんなご相談をいただきました。 「 図形の面積や体積の公式 が難しいです。 アルファベットとか出てくるし どうやったら覚えやすいですか?」 結論から言いますが、 暗記しよう!と思って力むと




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題
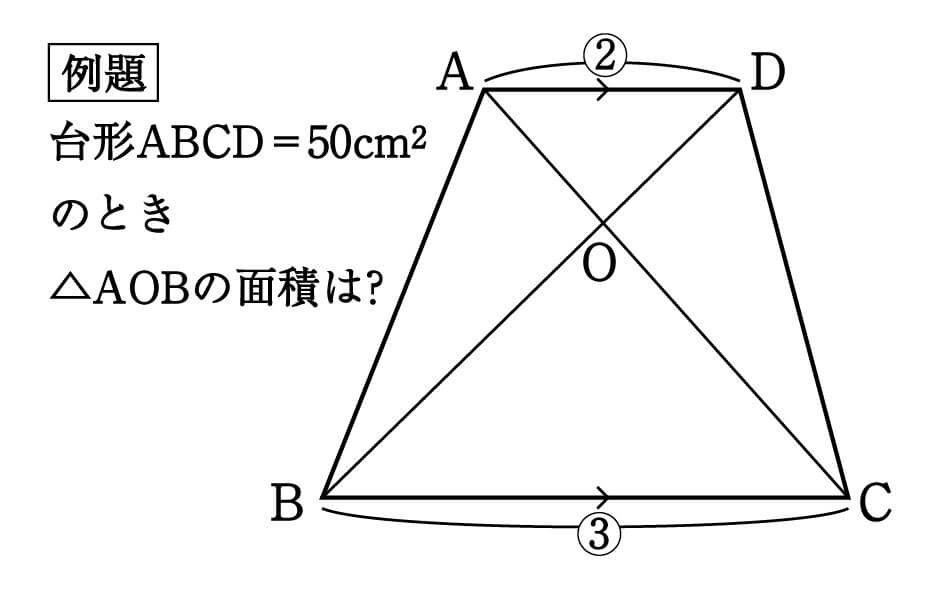



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
楕円の面積 の公式は、次ようになります。 楕円の面積 S=π・a・b 楕円は半径aの円を縦軸方向に b/a倍縮小(拡大)した図形 と考えることができます。 ですから、円の面積公式(π・r・r)の応用と考えると覚えやすいです。 上記が「図形」の面積等を求める「基本公式」になります。 基本だけの問題というのはあまり出ませんが、基本ができて いないと応用はできませんので、確実にきちんと覚えておき ましょう。 台形=(上底+下底)×高さ÷2 上記の台形の面積はPocket 中学数学で学習する重要な公式たちをまとめておきます。 入試や学力テストなど 大きなテストの前には、こちらの記事で公式をチェックしておきましょう (^^) こちらのページで紹介している 公式をまとめたプリントを無料でプレゼント! 印刷して




円の面積 練習応用 Youtube




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
台形の図形面積の公式は下記の通りです。 面積=(上底+下底)× 高さ ÷ 2 台形とは、「1組の向かい合う辺が平行になっている」四角形のことをいいます。そのため、正方形、長方形、平行四辺形も台形に含まれます。(1) 積分で面積を求めるうえで,重要なのは関数の上下と 交点の 座標の 2 つです。 まずはグラフをかいて面積を求める図形と, 2 つの関数でどちらが上に位置するかを把握しましょう。 面積を求めるのは灰色の部分ということがわかります。ここでは が の 上に位置しているので,面積の公式台形の面積が公式で求められる理由 2つの説明の仕方があります。 説明1台形2つで平行四辺形になる 台形と合同の図形を180度ひっくり返してくっつけたら平行四辺形になります。




中学 高校で習う三角形の面積公式 Memory Map 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



高校数学無料問題集 数 第3章 図形と計量 面積 桝 ます Note
図形の面積を求める公式を用いて面積を求める という流れになります。読む感じはやることが多そうですが、慣れてしまえば作業的に解くことが出来ます。 問題1 次の赤で塗られた部分の面積を求めてこれまでグラフで囲まれる部分の面積は、 「上のグラフ」-「下のグラフ」の定積分 で求めましたね。 もし、求める面積が 「放物線と直線」で囲まれる図形 である場合、実はとても便利な計算公式が利用できます。 さっそくその公式を紹介しましょう。長方形の面積の求め方はよく知っていると思います。 一番簡単な公式ですね。 長方形の面積=たて×よこ 特に問題はないですね?このあとにでてくる 平行四辺形 三 » この記事の続きを読む




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
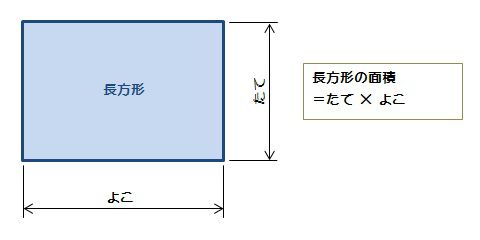



長方形の面積 算数の公式覚えてますか
・ 台形の面積=(上底+下底)×高さ÷2 ・ ひし形の面積=対角線×対角線÷2 面積の公式 ⑴ 三角形 ⑵ 平行四辺形 高さが三角形や平行四辺形の外にある図形でも,公式をつかって,図形の面 積をもとめる 図形を総まとめ! 小学校〜高校で習う各種公式重要記事一覧 21年2月19日 小学校から高校にかけて習うさまざまな図形に関する情報をまとめていきます。 公式・問題を解説した詳細記事へのリンクを載せていますので、ぜひ勉強の参考にして台形の1辺・面積(3辺の長さと高さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 ひし形の面積 平行四辺形の面積 (底辺と高さから) 平行四辺形の面積(底辺と高さから) 平行四辺形の面積 (2辺と夾角から)
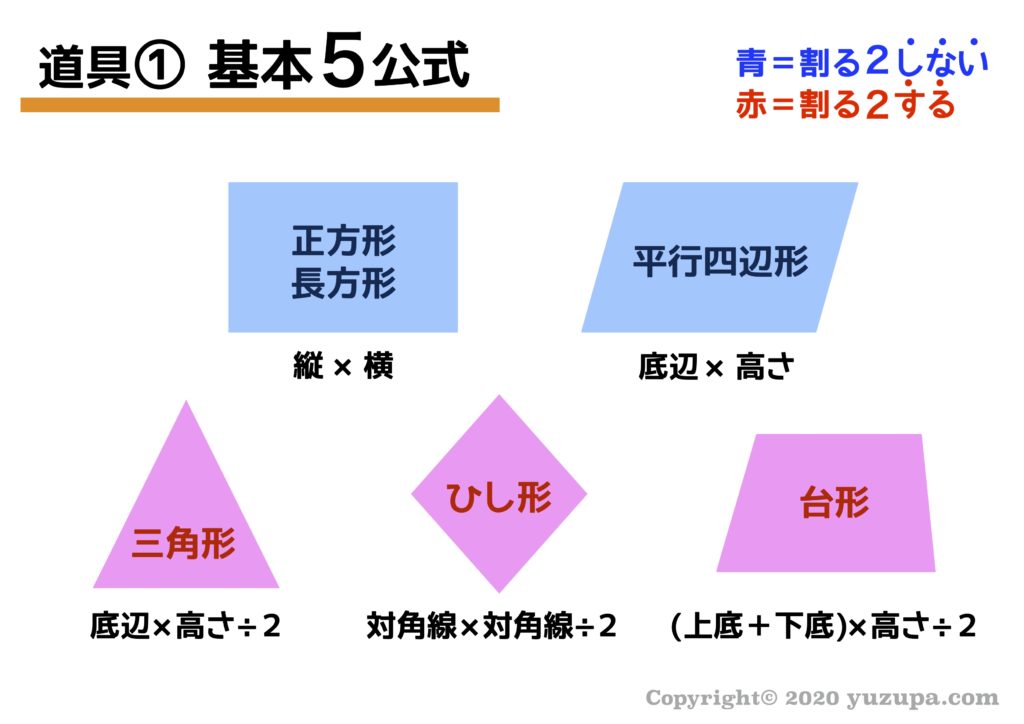



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
公式一覧 (画像目次) 1 角度の公式・考え方 2 長さの公式・考え方 3 面積の公式・考え方 4 等積図形・一覧 5 体積の公式・考え方 6 表面積の公式・考え方 7 図形と比の公式① 8 図形と比の公式② 9 体積と比の公式・考え方 10 水そうの公式・考え方 112角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい三角形の面積を求める公式 三角形の面積=底辺×高さ÷2 (ていへん かける たかさ わる2) 公式の理解ができたら、公式を覚える練習もさせましょう。 聞いてあげて下さい。 面積の表し方は、4年生の時に、マス目がいくつあるかを考えさせ、後に1㎠を教え
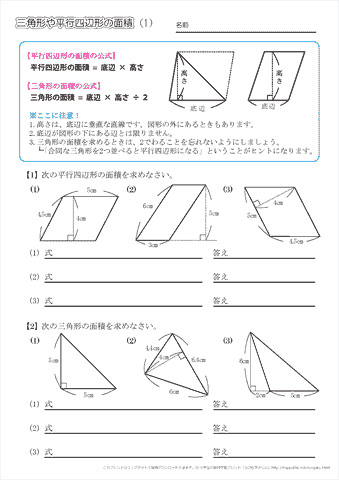



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
積変形の考え方のよさに 気付き、既習の公式 を使って複合図形の面積 が求められることに 気付く。 グループでの話合いで は、自分の考 えを高めたり、新しい考え方に気 付 いたりできるように適切な小学生|算数|公式の解説一覧|おかわりドリル ここでは、算数で使う公式で、なぜそうなるのか疑問に思いやすいものの解説を載せています。 公式などの解説のポイント ・ 公式を覚える際は、なぜそうなるのか? の疑問を解決すると覚えやすいですは、すでに「公式」としていろいろな図形の面積について学んでいることと思いますが、 もう一度その公式がなぜ成立するかを考えてみましょう。出発点は、 (長方形の面積)=(縦の長さ)× (横の長さ) です。この式をもとにして、 (平行四辺形の面積)=(底辺)×
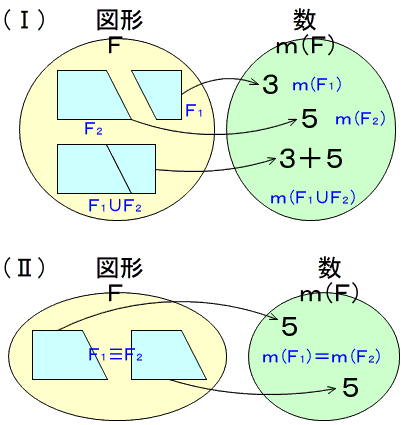



長方形の面積を求める公式の数学的な意味 Note Board




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
図形で使う公式・定理の一覧 扇の孤の長さ"l" 扇の半径をr、中心角をx、孤の長さをlとしたとき 扇の面積"s" 扇の半径をr、中心角をx、面積をSとしたとき 角柱の体積"vV = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は




平面図形の苦手を解消 三角形の面積比 基本編




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




小5 面積 三角形の面積の求め方 日本語版 Youtube
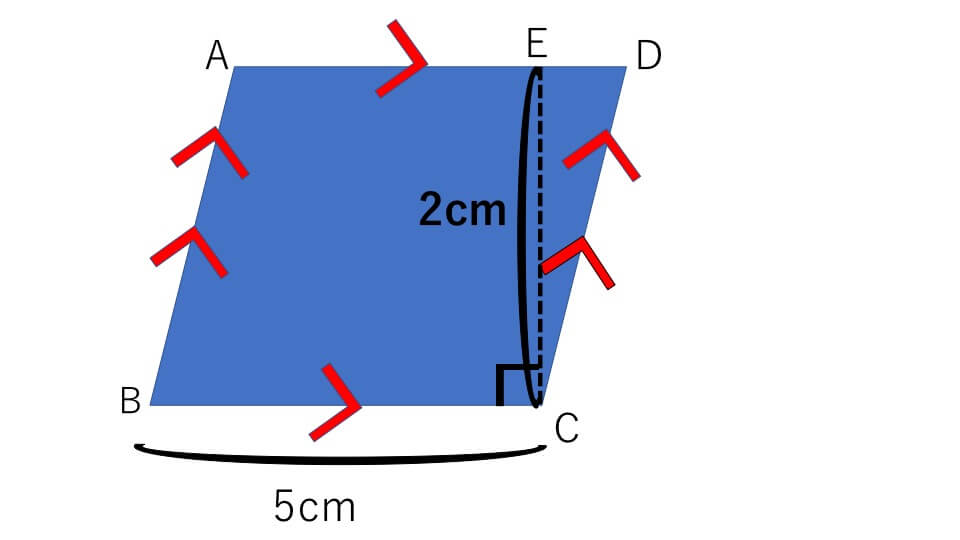



中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー




台形 の面積 計算ドリル 問題集 数学fun




裏ワザ公式 グラフ上の三角形の面積を一発で求める方法 Youtube




中学数学の図形で使う公式 定理の一覧 中学数学 By となりがトトロ マナペディア




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




高校数学 三角形の面積の公式 映像授業のtry It トライイット




球の表面積と体積の公式 数学fun
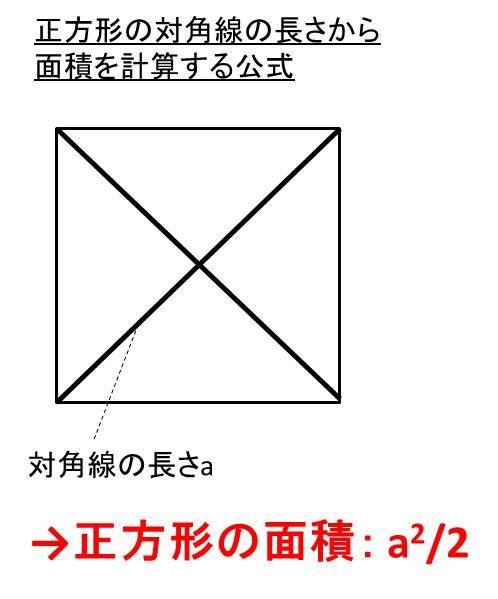



正方形で対角線の長さから面積を計算する方法 面積から対角線を求める公式 平方根 ウルトラフリーダム




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく



面積の求め方 算数の教え上手 学びの場 Com
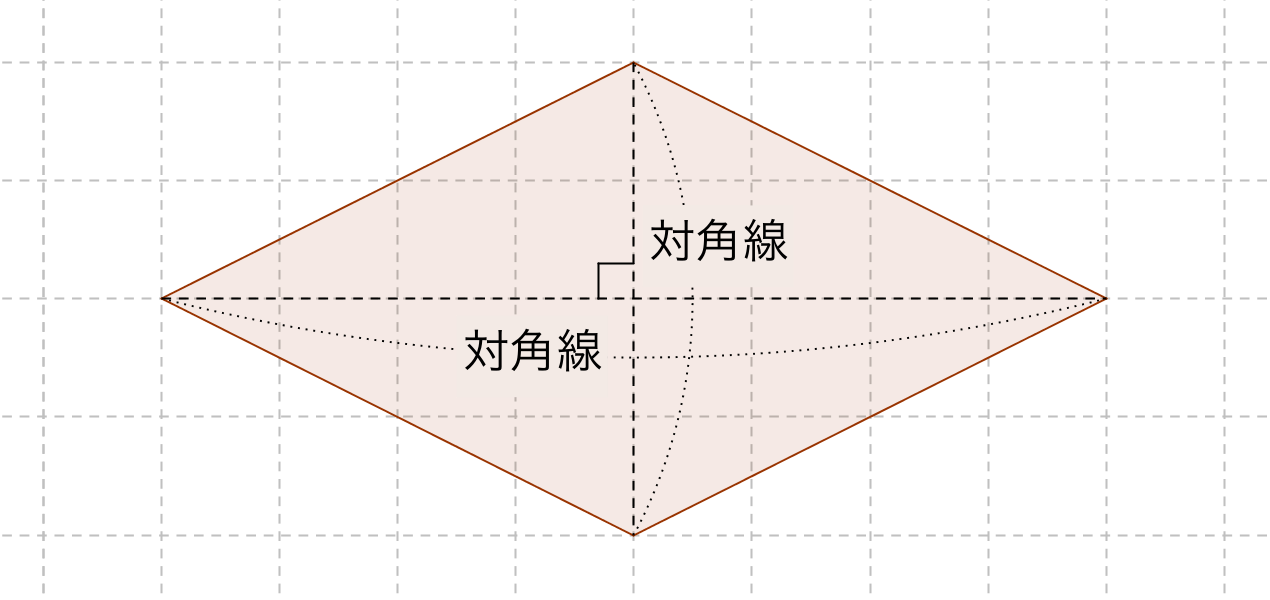



ひし形の面積の公式 算数の公式




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




この図形の面積の求め方を教えてください お願いします この図形 小学校 教えて Goo




面積の求め方 計算公式一覧




台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校




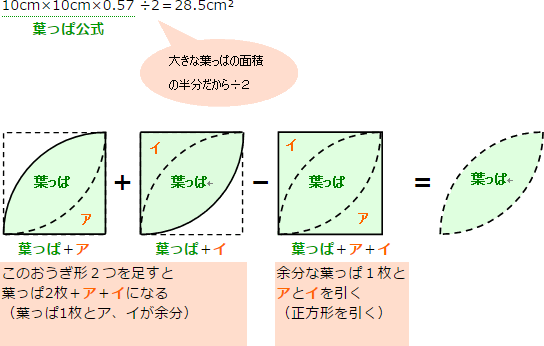
はっぱ型 の図形の面積 身勝手な主張
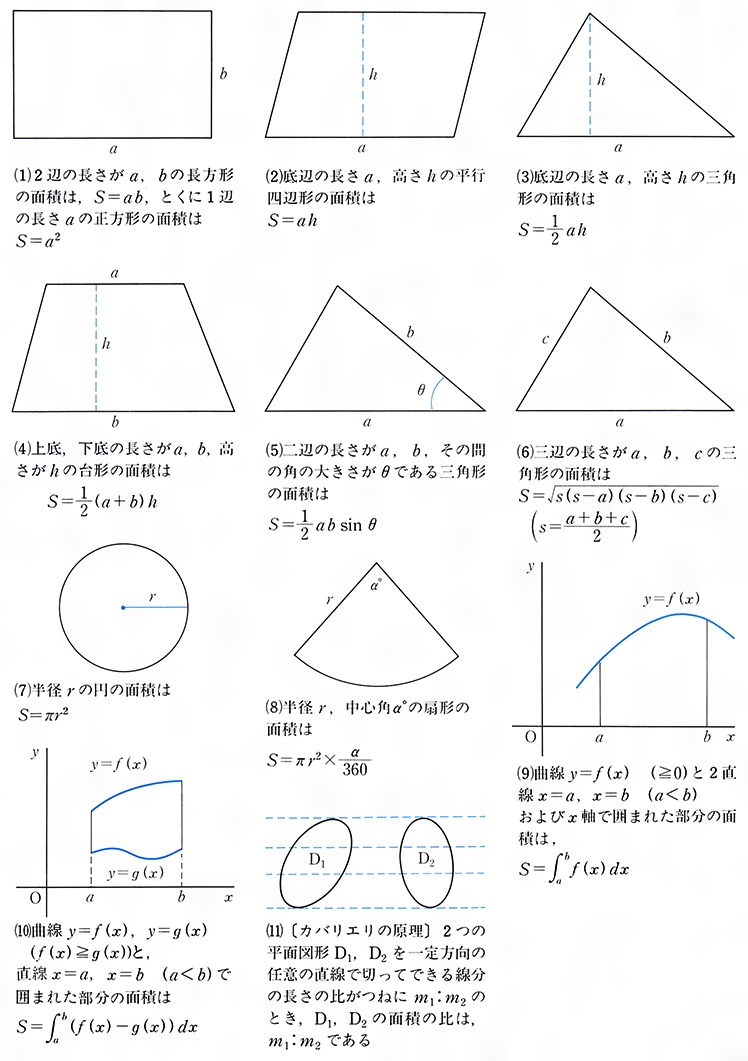



面積とは コトバンク




4つの乗法公式を図形の面積を求めることと考えてみよう 中3向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
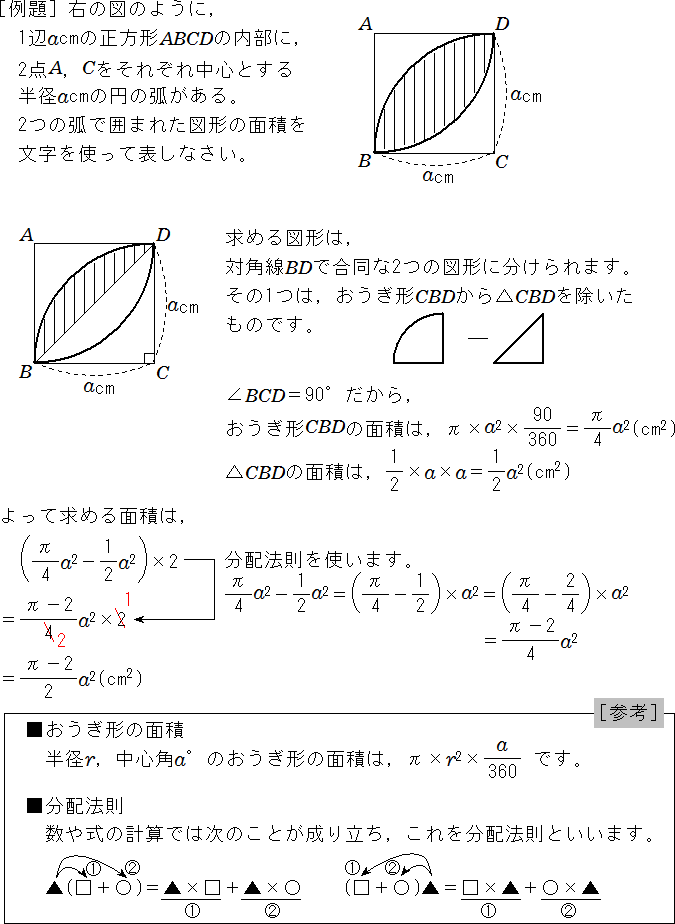



式の計算 文字を使った変わった図形の面積の求め方 中学数学 定期テスト対策サイト




平行四辺形の面積の求め方 公式と計算例




Amazon Co Jp 1枚で 平面図形 がわかる Learneasy 図形 を学ぼう 平面図形の種類と公式ポスター プチバイリンガル英語付き 大判a2サイズ 一覧表 小学生算数教材 文房具 オフィス用品




面積の求め方 計算公式一覧
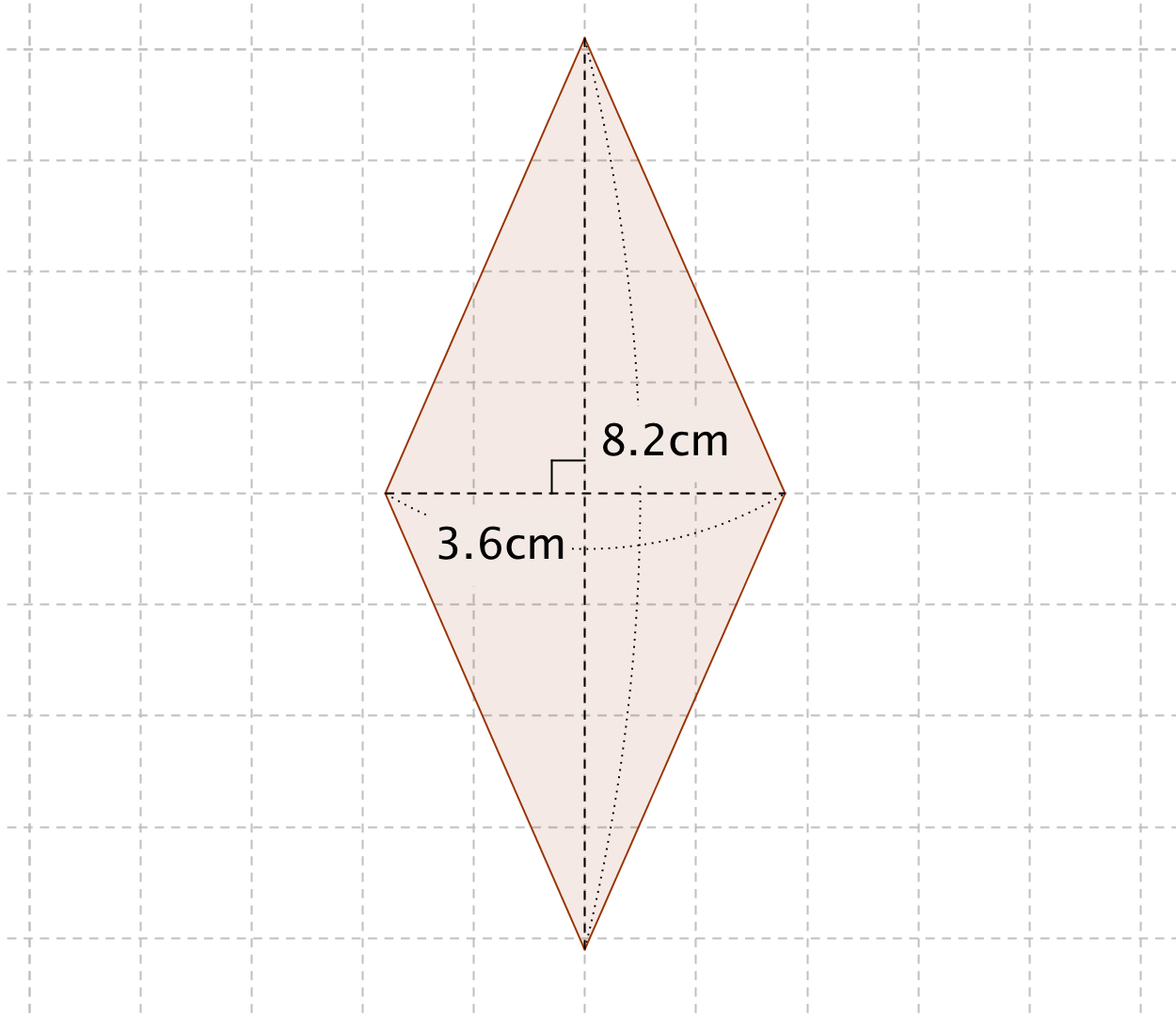



ひし形の面積の公式 算数の公式




表面積の求め方 計算公式一覧




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




表面積の求め方 計算公式一覧



U9j580gf8iba369ji2w Xyz P 296
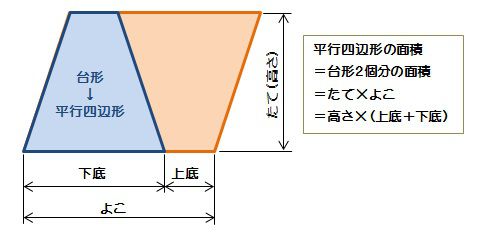



台形の面積 算数の公式覚えてますか



1




ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題
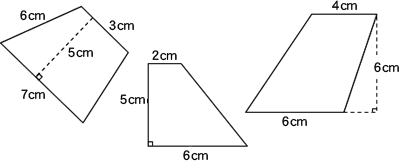



図形の面積 面積の求め方を考えよう 第5学年 小学校 算数 My実践事例 日本文教出版




平行四辺形の面積の求め方 公式と計算例




空間図形に含まれる三角形の面積を求める問題 直方体 数学i By ふぇるまー マナペディア




高校数学 座標平面上の三角形の面積の公式 受験の月
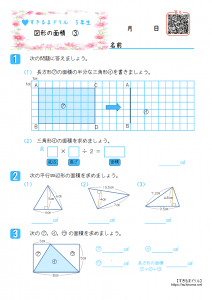



すきるまドリル 小学5年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント
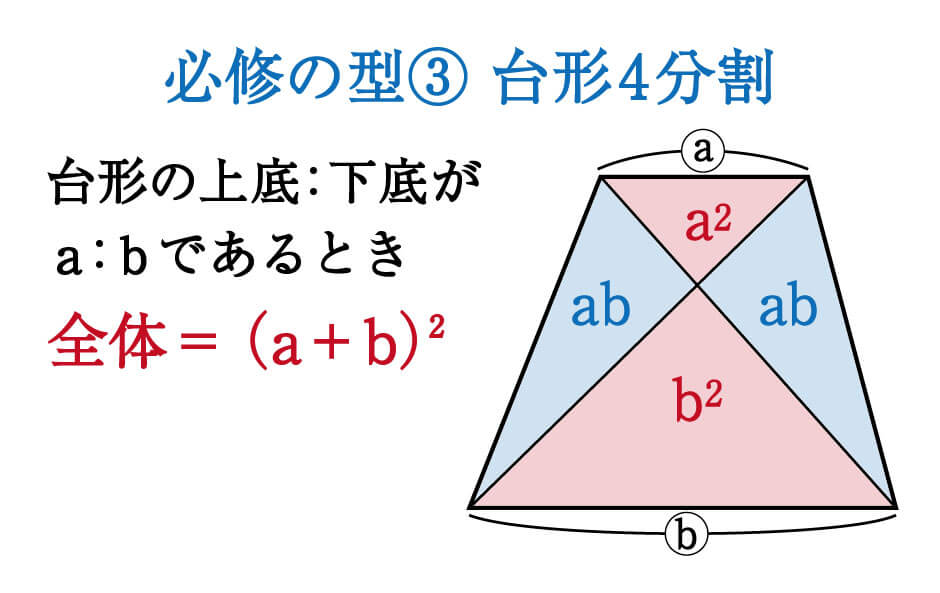



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
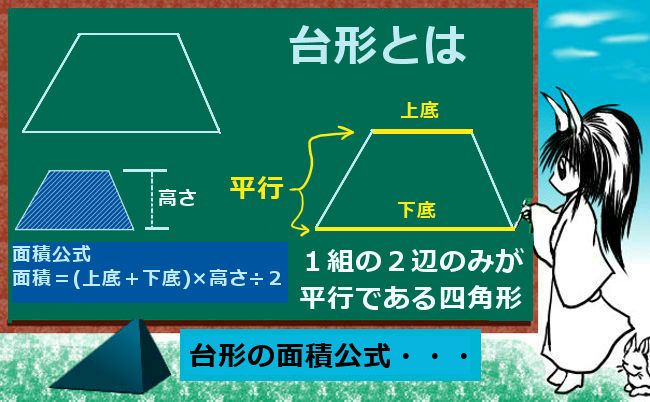



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori




体積 表面積まとめ記事 いろいろな図形の求め方を一気に学べる 高校生向け受験応援メディア 受験のミカタ



Spi M54e217p7lcis9d Com Category E5 9b E5 81 Ae E9 9d E7 8d




授業案解説 小5 算数 数学 B 3 平面図形の面積 雲雀丘学園小学校 小田 剛士先生 Youtube
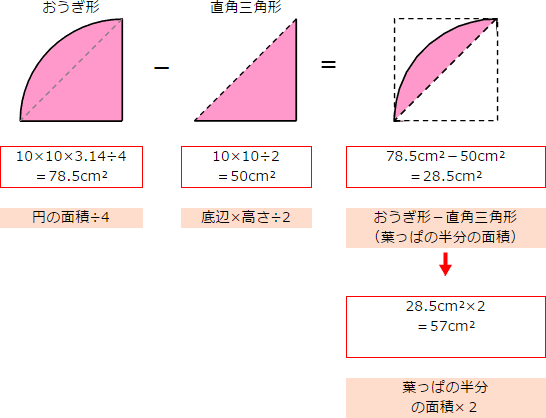



面積の求め方 算数の教え上手 学びの場 Com




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




長方形の面積の求め方 簡単な計算問題で公式を覚えよう 中学や高校の数学の計算問題



1
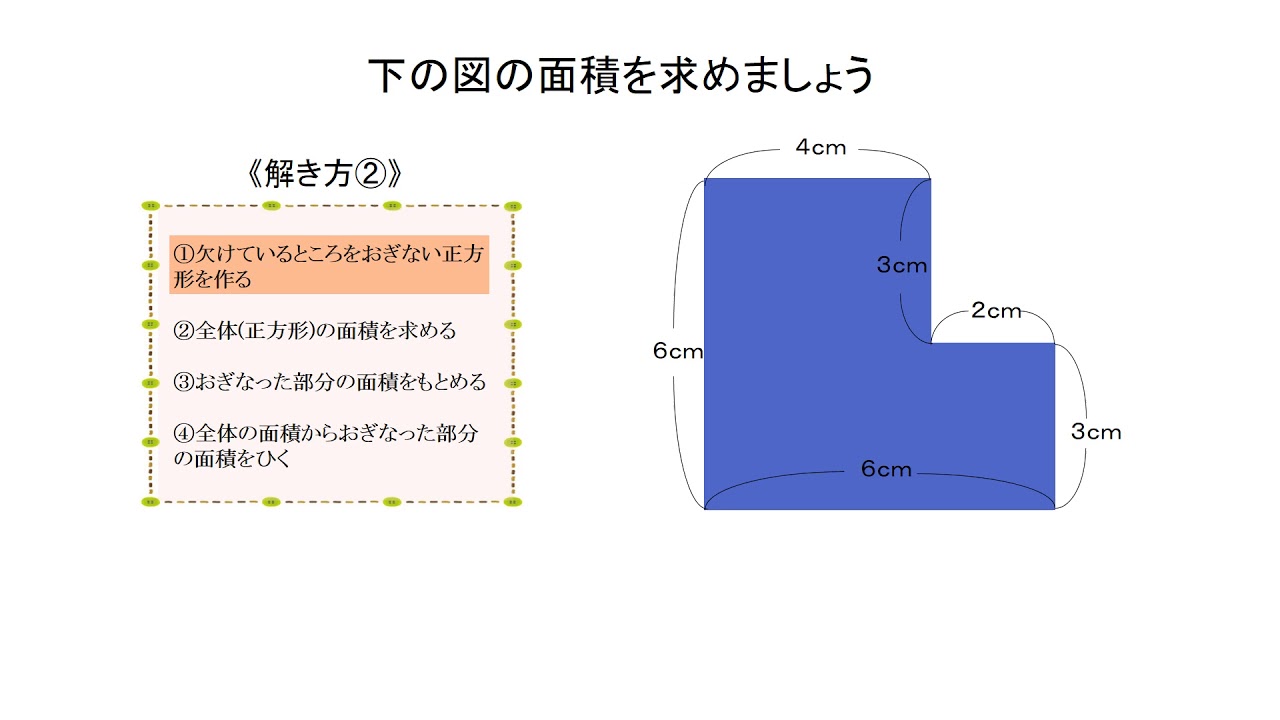



小4 面積の求め方の工夫 日本語版 Youtube
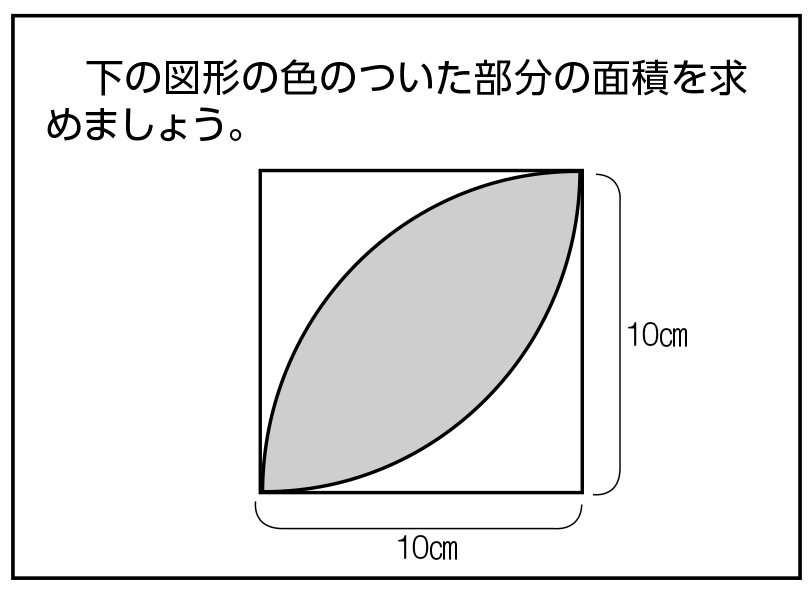



小6算数 円の面積 指導アイデア 2 みんなの教育技術
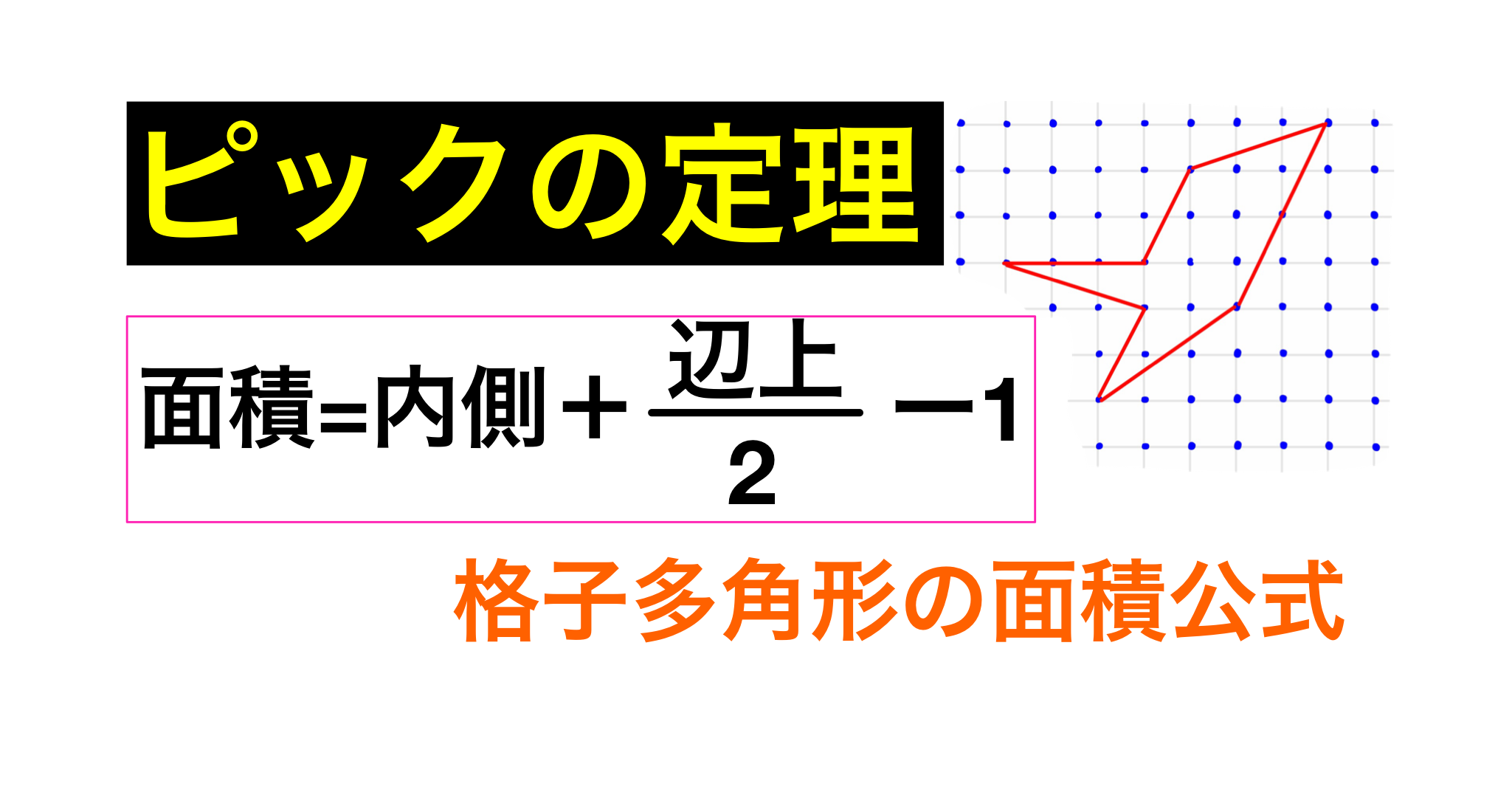



ピックの定理で 面積を簡単に計算 すうがくブログ 式変形ch




ボード 子供の教育 のピン




平行四辺形の面積の求め方 公式と計算例



ベクトルによる三角形の面積の求め方 公式や証明 計算問題 受験辞典




中1 中1数学 空間図形公式まとめ 中学生 数学のノート Clear
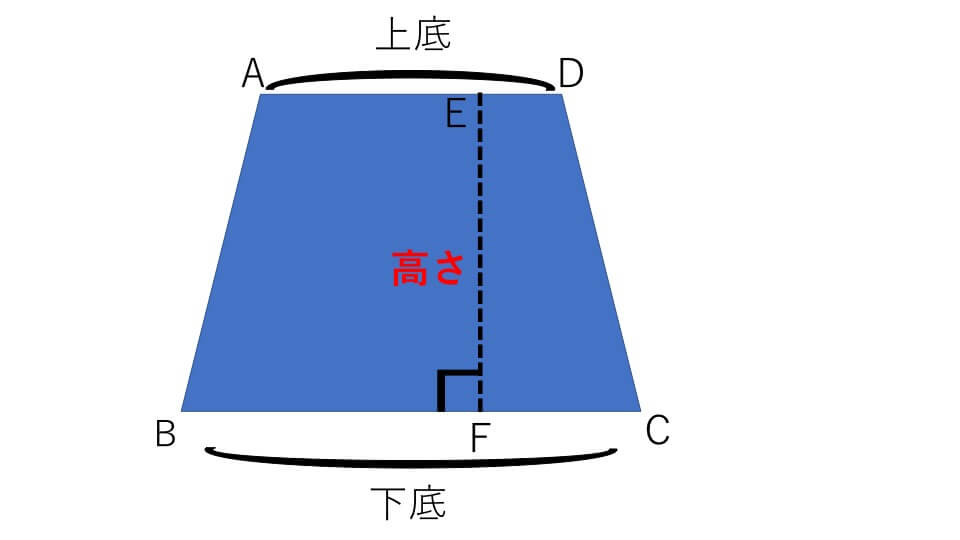



中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
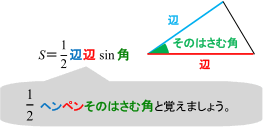



三角形の3辺が与えられたときの面積の求め方 数学 苦手解決q A 進研ゼミ高校講座
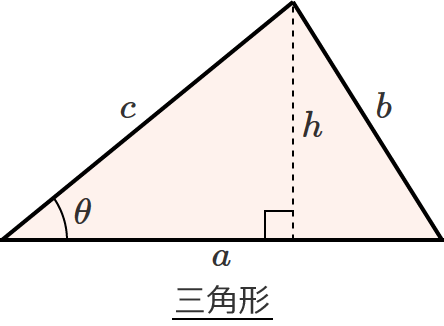



図形の面積を求める公式




高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




5年算数面積 教え方のポイント




6 柱と梁の断面形と幾何学
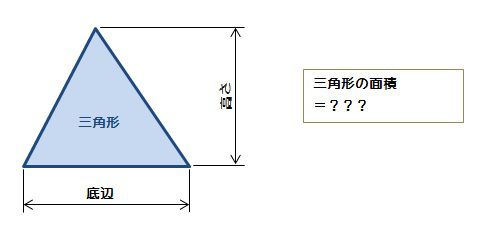



三角形の面積 算数の公式覚えてますか



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
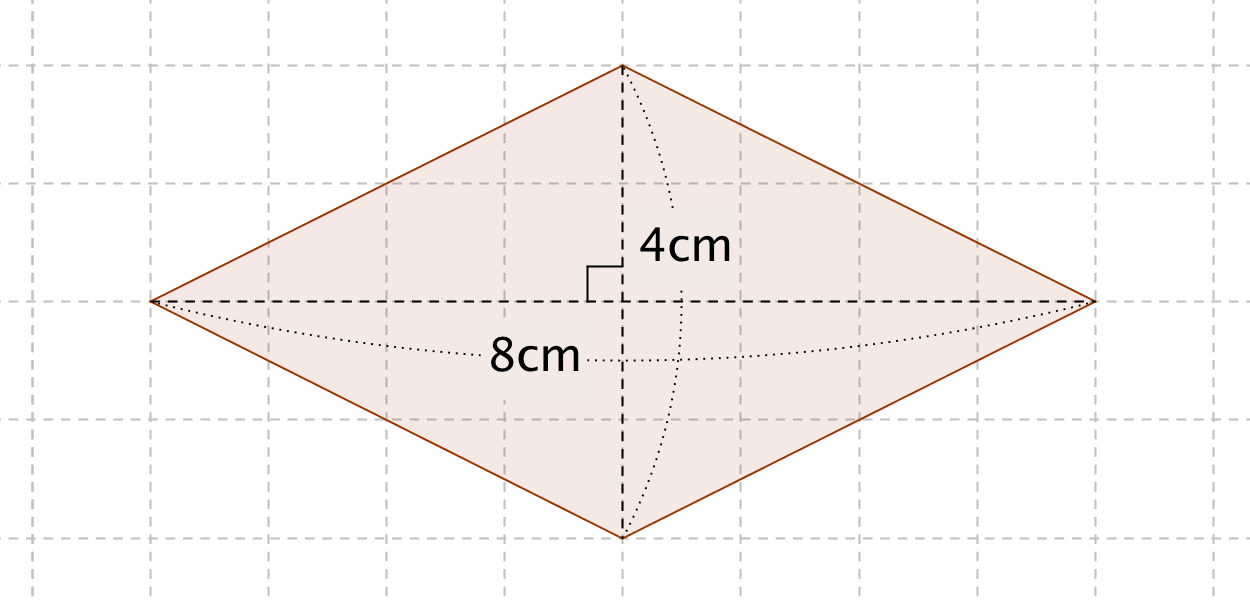



ひし形の面積の公式 算数の公式



3
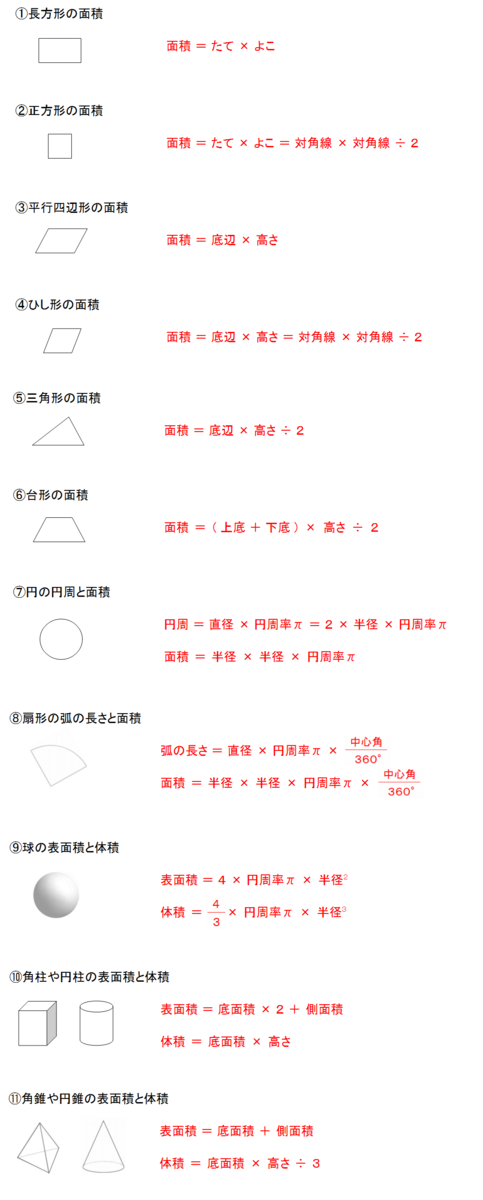



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




三角形の面積を求める公式7選 高校数学のまとめにどうぞ




角錐 円錐の体積と表面積の公式 数学fun



1
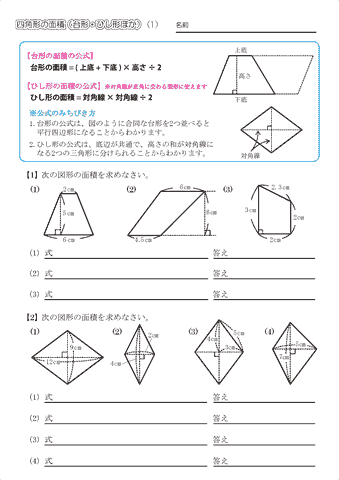



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生




直感的に求めよう 直角三角形の面積の求め方 パパが教える算数教室



250枚 至急 葉っぱ形の図形の面積について質問です Yahoo 知恵袋




授業案解説 小5 算数 数学 5年b 3 平面図形の面積 雲雀丘学園小学校 小田 剛士 Youtube




面積の求め方 算数の教え上手 学びの場 Com




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト




ボード 支援教材 のピン




面積の求め方 公式一覧 小学生 中学生の勉強




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear




平行四辺形の面積の求め方 公式と計算例




三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




平面図形の苦手を解消 三角形の面積比 基本編




ひし形 菱形 の面積の公式は 対角線 対角線 2 見やすい図で即理解 高校生向け受験応援メディア 受験のミカタ


