よって球の表面積は外接円柱側面の面積に等しい、 とう趣旨を主張している。 12 節回転体の体積 任意の面を軸の回わりに回転させた回転体の体積公式は、 西洋流ではバッポス = ギュルダンの公式と呼ばれる。関も、 と (3 において、公式を4) 「体積=面積※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= πr 3 を半径で微分すると表面積 S=4πr 2 になることが分かる.脱線ついでに言えば,円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる.表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 314
Fhpxqjuuu3lszm
球 の 表面積 の 求め 方 小学生
球 の 表面積 の 求め 方 小学生- 下図のように切り込みを入れてはがす。 横の長さ=球の一周分の長さ= 2πr 縦の長さ=球の半周分の長さ= πr 形を単純にしてだいたいの面積を求める. 面積= πr × 2πr × 1 2 = π2r2 = 314πr2 形を切り落として考えているため,実際の面積はもう少し大きいと考えられる. 球体の表面積 S > 314πr2 (1)球の表面積がそれに接する円柱の側面積に等しいのは、微小部分を円柱に投影したとき 任意の位置でスライスした(正確な半球でないもの)場合の表面積の求め方 を 上記では、球冠の側面積を重積分で求めたが、高校の数学Ⅲの範囲で十分求め




Descubre Como Resolverlo En Qanda
なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。球冠,球帯の面積の求め方01 一点から発せられた光をあるnaを持つ対物レンズで取り込む,そのときにnaによってどの程度の明るさが異なるか,など気になりますね. いろいろなサイトに,naと明るさの関係の記述があります(オリンパス).N次元球の表面積と体積の求め方。 こちらでで触れたガンマ関数(Γ Function)の応用例。 Python演算処理階乗と順列と組み合わせ 正直私にとってはパラダイムシフトでした。
球の体積と表面積 東京大学大学院数理科学研究科・教授 古田幹雄 1 円の面積と円周の長さ 半径rの円の面積はˇr2 です。 グラフv = ˇu2 のu = rにおける接線の傾きを求めてみま す。すると、答えは2ˇrとなります。これは半径rの円周の長さです。つまり、円の面積球の表面積 球の表面積 = 半径×半径×4×314 この公式を,パップス・ギュルダンの定理を利用して,小学生レベルで導いてみます。 パップス・ギュルダンの定理による表面積の考え方 回転させたい図形を, (とても細い)針金でできていると考える 球体の表面積S = 4πr 2
表面積 (上辺・底辺含まず) S = π (2 r h 2 r 2 − h 2)よって,球帯の表面積は S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ S=2\pi r^2\int_{\theta_1}^{\theta_2}\cos\theta d\theta S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ (ただし, θ 1 \theta_1 θ 1 は球帯の底面の緯度, θ 2 \theta_2 θ 2 は球帯の天面の緯度)立体角は、半径1の球(単位球)の一部の面積で定義されていました。単位球の表面積は $4\pi$ なので、立体角は、$0$ 以上 $4\pi$ 以下です。 「$4\pi$ ステラジアン」は「全方位」に対応する立体角です。 立体角の計算例
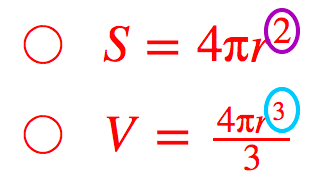



球の表面積と体積の求め方 苦手な数学を簡単に



3
球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。次に、球の表面積の公式の求め方について考察する。 まずは体積のときと同様にすると、図1において、 球の中心から距離 xの点で切った断面である円の 円周の長さは、L(x)=2π√(r2-x2)となる。 よって、球の表面積Sは、円周をx 方向に積分すると、 S=2∫0r2π√(r2-x2) dxより、 x=rsinθ と置換すると、S=4π∫0(π/2)√(r2-r2sin2θ)rcosθ dθ =4πr2∫0(π/2)cos2θ dθ=4πr2 LINE Pocket 今回は中1で学習する「空間図形」の単元から 球の体積・表面積の求め方について解説していくよ! 球というのは こういったボール状の形をしているものだよね! 実は、ちょっとだけ公式が複雑だったりします (^^;



中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su



球の表面積の公式の求め方
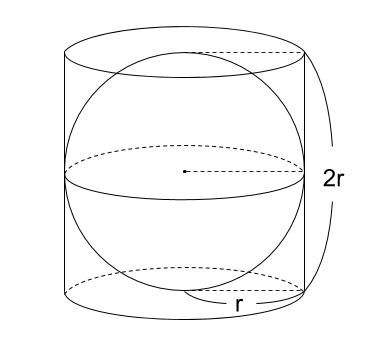
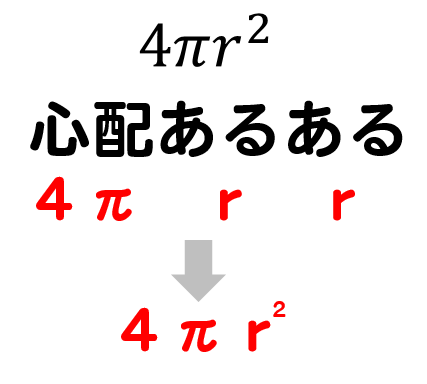
1/2時 ・球の体積を求めることができる。 ・球の体積の求め方を理解する。 球の表面積の求め方を復習する。 本時の学習内容「球の体積の求め方を考えよう」を知る。 教科書180ページの「ひろげよう」に取り組む。 何杯分になるかを予想する。 全体の場で、代表者が半球と円柱の模型を使って実験を行う。 円柱には半球の3杯分の水が入ることを確認する。球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するための語呂は、




球体の表面積 積分で求める方法 うちーノート




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
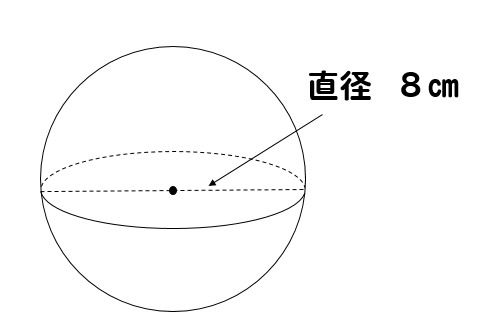
表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。楕円錐台の底面と上面の半軸と高さから体積、側面積、表面積を計算します。 球の体積 球の体積 球の半径から体積と表面積を計算します。 一部が欠けた球の体積 一部が欠けた球の体積 一部が欠けた球の体積と表面積を計算します。 次に、円柱の表面積の求め方は「底面積 × 2 側面積」なので、式は「4π × 2 側面積」。 また、 円柱の側面積の求め方は 「高さ × 円周」、 円周の求め方は 「直径 × π」なので、式にすると 4π × 2 8 × 4π = 40π




初等幾何 球の表面積を求める 大人が学び直す数学




中1 数学 6 5 球の体積 表面積 Youtube
数学 球 表面積 求め方 球体の表面積 中学生に分かるように真剣に考えてみた うちーノート 球の体積 表面積 無料で使える中学学習プリント 中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく 球の表面積の求め方 うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめています。 前回の記事(Part26)はこちら! 広義積分・ガウス積分に球の表面積の場合は、 球面の全てを覆うように積分範囲を指定する必要があったが、 弓形領域の半分の領域 弓形領域の半分の領域 (黄色) の面積を求める場合は $\phi$ に関する積分範囲を $\alpha$ にすると、その領域が覆われる。




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



数学 球の表面積を積分で計算してもうまくいかない人へ
それは、「球の表面積の求め方の公式」 S=4πr×r(rの2乗が表記できないので)、球の表面積を求めるこの公式は覚えてました。 ところが教科書を予習していて見つけた、この言葉 「何々、『球の表面積は、その球がちょうど入る円柱の側面積に等しい r r の球の表面積は S=4\pi r^2,\ S = 4πr2, 球の体積は V=\dfrac {4} {3}\pi r^3 V = 34 πr3 である。 中学数学球の体積の求め方の公式を1発で覚える方法 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
球の体積の求め方(公式)の次は、球の表面積の求め方(公式)を学習しましょう。 下の図のように、 半径rの球があるとき、球の表面積は、4πr 2 となります。た円の面積や球の体積・表面積を求めるための公式と して生徒は受け止め,これらの式を暗記すればよいと みる傾向が強い。 円の面積,球の体積や表面積の公式を導く過程には, 様々な数学的なアイデ




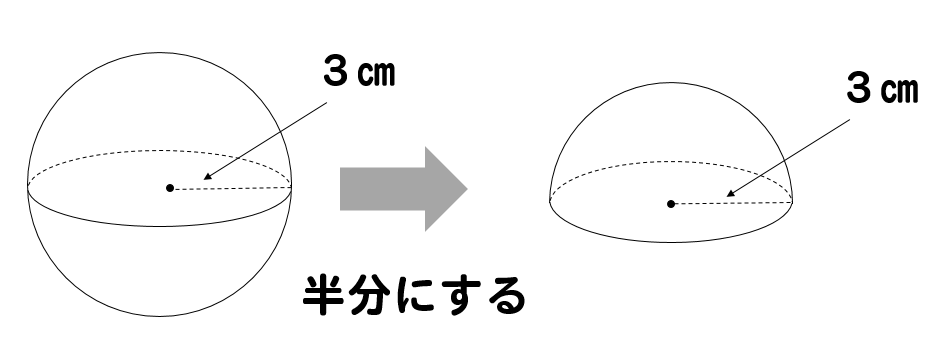
簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



1



4次元物体の表面積はどうやって計算するのですか Quora



Fhpxqjuuu3lszm




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球の体積 球の表面積の公式の導出 積分 優技録



球の表面積の公式の求め方



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




表面積の求め方 計算公式一覧




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の表面積の公式について みたにっき はてな



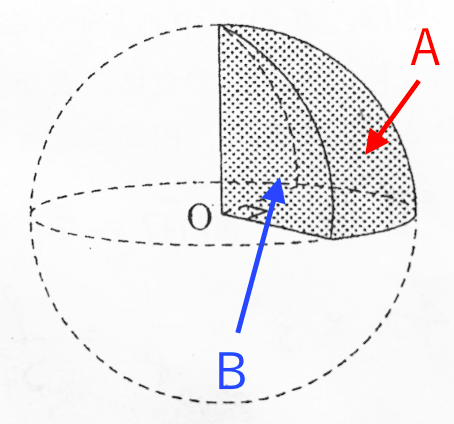
この画像は半径6 の球を 中心を通る平面で4等分してできた立体のうちの一 Yahoo 知恵袋



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の表面積と体積の公式 数学fun




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球の表面積と体積の求め方 苦手な数学を簡単に




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球の表面積の公式について みたにっき はてな
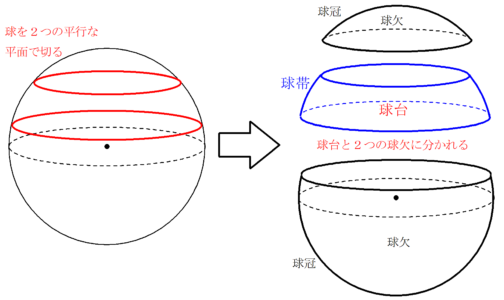



球台と球帯 Fukusukeの数学めも




2 を教えてください Clear



2




球の表面積と体積の公式 数学fun



立体 の 表面積 求め 方
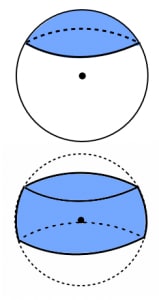



球欠 球台の体積と球冠 球帯の表面積 高校数学の美しい物語
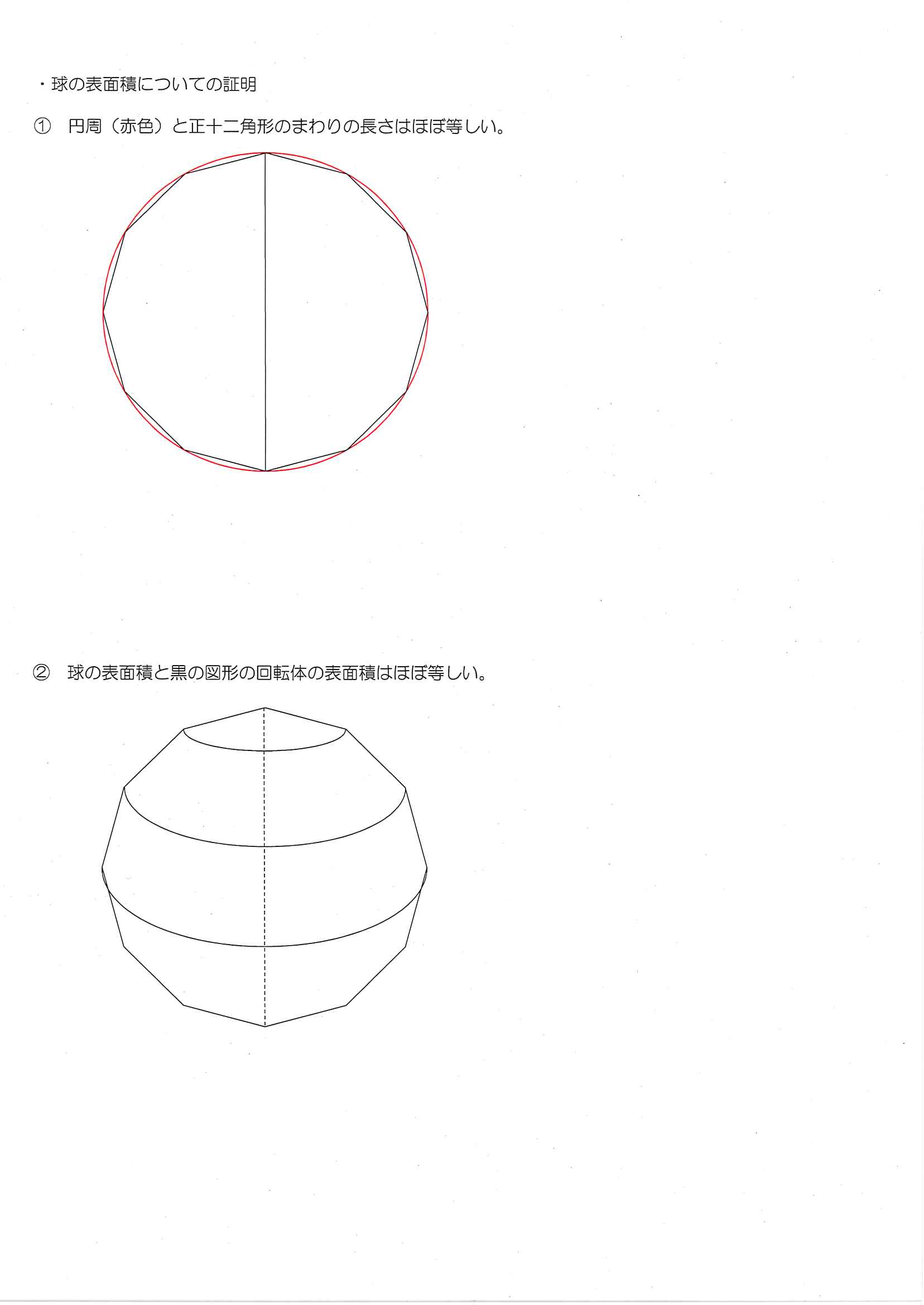



球の表面積の求め方 中学受験塾act アクト のブログ



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ
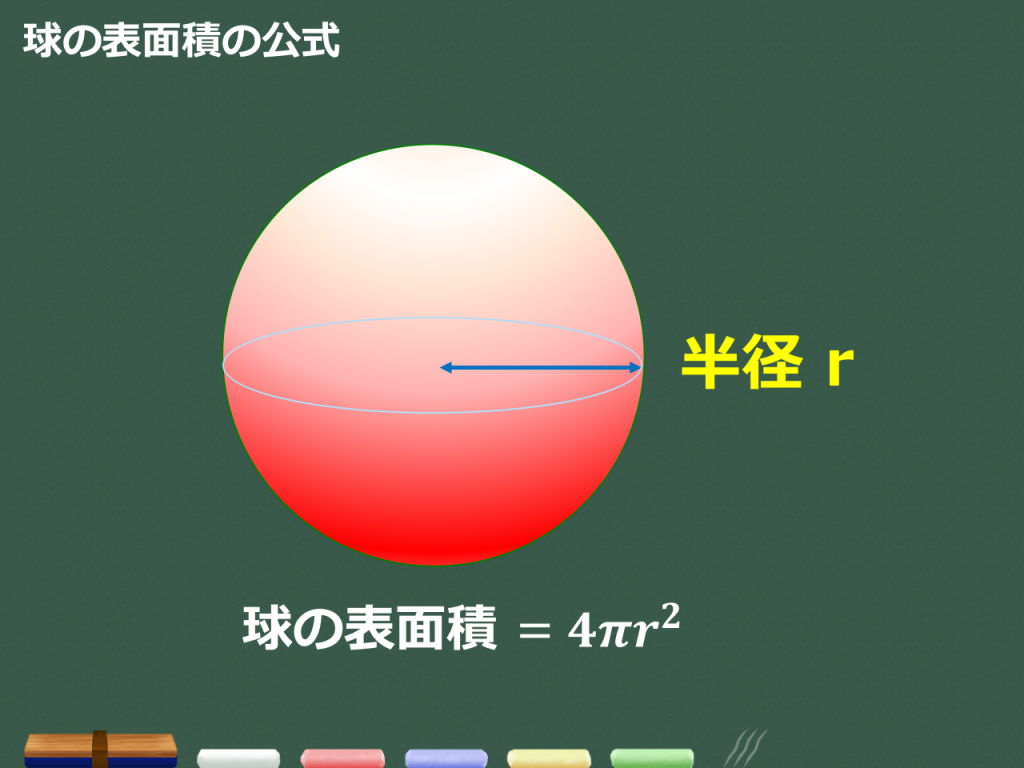



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ
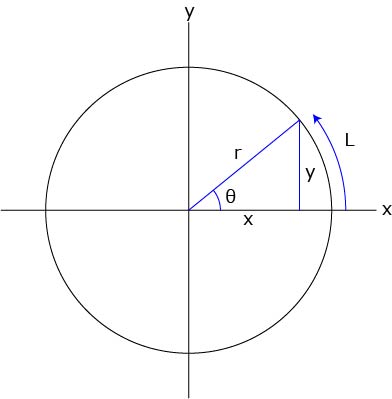



Sphere 01




Descubre Como Resolverlo En Qanda




球の表面積と体積の公式 数学fun




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球の表面積 簡単に計算できる電卓サイト



球の問題 苦手な数学を簡単に




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ




Mathematics 球の体積と表面積を求める公式 働きアリ




球の表面積の求め方 その3 感じる科学 味わう数学




公式一覧 立体の体積 表面積の求め方 円柱 三角柱 円錐 三角錐 球
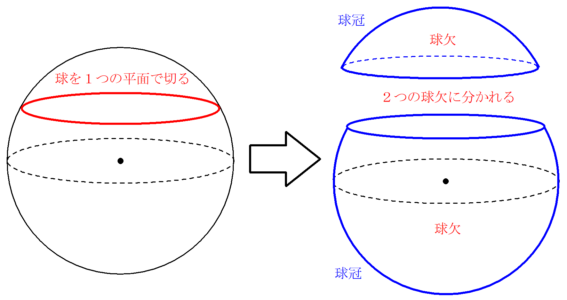



球欠と球冠 Fukusukeの数学めも




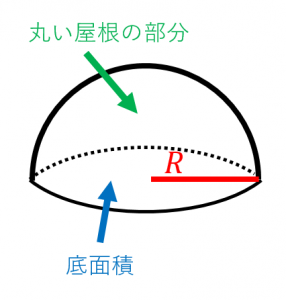
半球の体積と表面積を計算する 具体例で学ぶ数学



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




角錐 円錐の体積と表面積の公式 数学fun



Sphere 01



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




ここの 4 と 5 の体積と表面積の求め方教えてください Clear




中1 数学 中1 84 球について Youtube




球の体積と表面積 公式と計算問題と証明 Irohabook




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題




3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球の表面積 体積 身勝手な主張




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球面積 球の體積 Juliech



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




中1数学 球 例題編 映像授業のtry It トライイット



1




Excel エクセルで球の体積と表面積を計算する方法 モッカイ



半球の体積と表面積を計算する 具体例で学ぶ数学



球帯と球冠




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



円と球の求積 直感的方法




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋




球の体積公式の微分が表面積になっている理由 Youtube



1




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



大学入試問題




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球の表面積の求め方 公式と計算例




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




球の体積 表面積の求め方 公式 小学生 中学生の勉強




球の体積と表面積 Youtube




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



数学 球の表面積を積分で計算してもうまくいかない人へ




球の体積と表面積 Jsciencer




球の表面積 体積 身勝手な主張




球の表面積と体積の公式 数学fun



研究



Math 円柱 内接する球 円錐の体積と表面積 働きアリ
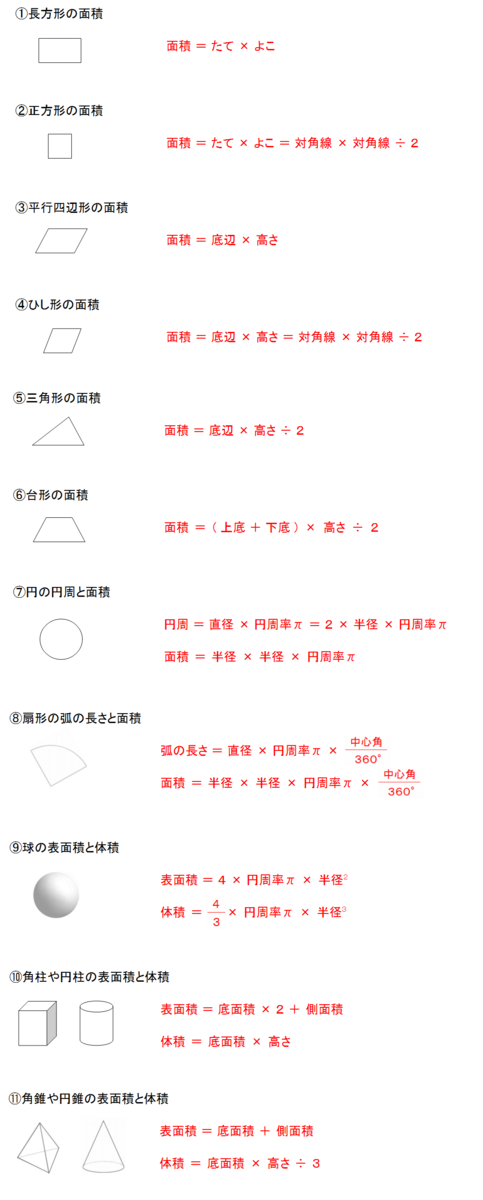



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典


