Click here to see ALL problems on Vectors Question a)Find the unit vector from the point P=(3,1) and toward the point Q=(18,9) b)Find a vector of length 34 pointing in Vector P Vector Q = Vector R and P=Q=R then find the ratio of angles between Vector P&R to Vector P&Q 1 See answer manimeghana400 is waiting for your helpRespectivelyP (1, 2, 3) Q (4, 5, 6) (𝑃𝑄) ⃗ = (4 – 1) 𝑖 ̂ (5 – 2) 𝑗 ̂ (6 – 3) 𝑘 ̂ = 3𝑖 ̂ 3𝑗 ̂ 3𝑘 ̂ ∴ Vector joining P and Q is given by (𝑃𝑄) ⃗ = 3𝑖 ̂ 3𝑗 ̂ 3𝑘 ̂ Magnitude of (𝑃𝑄

Find The Unit Vector In The Direction Of Pq Vector Where P And Q Are The Points 1 2 3 And 4 5 6 Youtube
What does p and q mean
What does p and q mean-And qis false However, if pis true and qis false, then p^qwill be true Hence this case is not possible Case 2 Suppose (p!q) is false and p^qis true p^qis true only if pis true and qis false But in this case, (p!q) will be true So this case is not possible either Example 10 Find the vector joining the points P(2, 3, 0) and Q(–1, –2, –4) directed from P to Q Given P (2, 3, 0) Q (–1, –2, –4) Vector joining P and Q



Q Tbn And9gctsezf Wnftk3ffjh7za7g1uuuz0uvxp6tgviupbup 79nnvg L Usqp Cau
The position vectors of points A and B are vec a and vec b respectivelyIf P divides AB in 3 1 internally &Q is midpoint of AP then point vector of point Q is Updated On To keep watching this video solution for32 If a dot product of two nonzero vectors equals1, then the vectors mustOr "either ¬P or Q" (if ¬P is false, then Q has to be true if the constraint is to be satisfied) In this respect, we can think of "satisfying the constraint P ⊃ Q" as being something like a theory about how the world is
The previous paragraph discussed a vector product that did not produce a zero vector, and therefore has a direction In the following discussion suppose that the vector product p x q is not the zero vector Then by 21 or by 12f, neither pnor q can be zero vectors, and the angle θ cannot be 0° nor 180° (meaning p and q cannot be parallel)If a parallelogram is constructed on the vectors apqbpqandpqa¯=3p¯q¯,b¯=p¯3q¯andp¯=q¯=2 and angle between pandqp¯andq¯ is π3, and angle between lengths of the sides is 713Answered 2 years ago Author has 340 answers and 14K answer views Given, PQ= PQ => PPQQ= O where O is zero vector => 2 Q= O => Q= O Thus Q should be zero vector only then it is possible If you are thinking to solve as, PQ ^2= PQ^ 2 P^2Q^22PQcosø= P^2Q^2–2PQcosø where ø is angle b/w P and Q
Let the position vectors of two points P and Q be \(3\hat{i}\hat{j}2\hat{k}\) and \(\hat{i}2\hat{j}4\hat{k},\) respectively Let R and S be two points such that the direction ratios of lines PR and QS are (4, –1, 2) and (–2, 1, –2), respectively Let lines PR and QS intersect at TPackage Loose Leaf for Vector Mechanics for Engineers Statics with 2 Semester Connect Access Card (11th Edition) Edit edition Problem 35P from Chapter 3 Given the vectors P = 2i 3j – k, Q = 5i – 4j 3k, and S =By law of vector addition, the resultant vector can be given as R = P Q Now when Q is doubled the new resultant vector can be given as R' = P 2Q since, R' is perpendicular to P hence there dot product should be zero or, R' P = 0 or, ( P 2Q ) P = P 2 2QP = 0




If Vecp Vecq Then Which Of The Following Is Not Correct




Vectors P Q And R Have Magnitude 5 12 And 13 Units And P Q Is Equal To R If Angle Between Q And R Is Brainly In
Match the vectors p^vector, q^vector, r^vector, s^vector, and t^vector with one of the combinations of the u^vector and v^vector vectors from the graph Question Match the vectors p^vector, q^vector, r^vector, s^vector, and t^vector with one of the combinations of the u^vector and v^vector vectors from the graph Magnitude Sum of Two vectors Vector P and Vector q is given by r^2 =p^2q^22pqcos($) _____(i) here $ indicates angle between them We are given r=pq so Squaring both the sides we get r^2=p^2q^22pq _____(ii) From (i) and (ii) we can write p^2q^22pqcos($)=p^2q^22pq therefore 2pq=2pqcos($)Because Q is our endpoint and P is our starting point And when we do this, the resulting vector is the following to I'm sorry to minus one is one to minus one, this one and zero minus negative Five It's five, so we get 115 and that again is P Q And then PR will be ar minus P And so we get zero 00 minus 11 negative five and the resulting




The Angles Between P Q And P Q Will Be Youtube



What Are The Conditions Under Which Two Vectors P And Q Are Perpendicular To Each Other Quora
Show vector (pq) is orthogonal to the curve at q Let f R → R n be a differentiable mapping with f ′ ( t) ≠ 0 for all t in R Let p be a fixed point not on the image curve of f If q = f ( t 0) is the point of the curve closest to p, that is, p − q ≤ p − f ( t) for all t in R, show that vector ( p − qThe dot product of two vectors P and Q, when placed tail to tail make an angle θ, can be written as 30 The dot product of two vectors results in what type of quantity? two boats p and q are at points whose position vector are 4i8j and 4i3j respectively both of the boats are moving at a constant velocity of p is 4ij and q is 2i5j find the position vectors of p&q and pq after t hours, and You can view more similar questions or ask a



If The Resultant Of Two Vectors P Q Is P Q Then Angle Between P Q Is Quora




Resultant Of Two Vectors Of Magnitude P And Q Is Of Magnitude Q If The Magnitude Of Vecq Is Doubled Now The Angle Made By New Resultant With Vecp Is
Find stepbystep Precalculus solutions and your answer to the following textbook question Express the vector with initial point P and terminal point Q in component form P(8, 6), Q(1, 1)The resultant vector P and Q is Ron reversing the direction of the angle the resultant becomes Sshow that R sqS sq=2(P sqQ sq) Post Answer Answers (1) A If the radius of its base is R and its height is h then z0 is equal to Q Need explanation forAnswer to Find the x and y components of the following vectors P 23 m, at 16 degrees counterclockwise from x Q 21 m, at 86 degrees



Q Tbn And9gcsk9dx33rh Eq1qxdb76gs Lcj3xg6 Qt7xiazntjdlk37yxdqo Usqp Cau




The Resultant Of Two Vectors P And Q Is R If Q Is Doubled T Scholr
If p ˄ q = F, p → q = F, then the truth value of p and q is Maharashtra State Board HSC Science (General) 12th Board Exam Question Papers 231 Textbook Solutions Online Tests 73 Important Solutions 3704 Question Bank Solutions Concept Notes & Videos & Videos 721(1)theta1=theta2 (2)theta1=theta2/2 (3)theta1=2theta2 (4)none of these if `PQ=PQ` ,then Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan Vectors if PQ=PQ ,then Watch 1 minute video Updated On 16 To keep watching this video solution for



The Sum Of Two Forces Vector P And Q Is Vector R Such That Vector R P The Angle 8 In Degrees That The Resultant Of Vector 2p And Q Sarthaks Econnect




8 If P And Q Are Two Unit Vectors And The Angle Between Them Is 60 Then Is 1 2 P Q D2 1 2
Let the angle between two vectors P and Q be alpha and their resultant is R So we can write R2P2Q22PQcosalpha1 When Q is doubled then let the resultant vector be R_1 So we can write R_12P24Q24PQcosalpha2 Again by the given condition R_1 is perpendicular to P So 4Q2P2R_123 P = ( 5, 11) and Q = ( 6, 4) The vector QP is equivalent to the directed line segment " P Q " = < 1, 7 > When, we write < >, we mean that The vector has initial at the origin and terminal point at (1, 7) This notation is called the component form of the vector The length of the vector is called the magnitude esultant of two forces P and Q is R R = P Q R = sqrt(P^2 Q^2 2PQCosθ) When Q is doubled new resultant R' is R' = P 2Q Since it is perpendicular to P, dot product of R' and P is zero (R')(P) = 0 (P 2Q)(P) = 0 P^2 2PQCosθ = 0 (Dot product of P and P is P^2 and that of P and 2Q is 2PQCosθ) Cosθ = P/(2Q) R = sqrt(P^2 Q^2 2PQCosθ) R = sqrt(P^2 Q^2 2PQ*(P




Two Vectors P And Q Of Equal Magnitude Make An Angle 64 With Each Other What Is The Angle Made By P Q Brainly In




P Q Is A Unit Vector Along X Axis Ifp I I K Then What Value Is Q A 1 1 K B C 1 1 K D 1
If a, b, c are in AP then 2b = a c If a, b, c are in GP then \(\rm b^2 = ac\) Calculation Given p, q, r are in AP as well as GP Now, p, q, r are in AP ⇒ 2q = p r (1) Again, p, q, r are in GP ⇒ q 2 = pr (2) By equating (1) and (2) we getThe resultant of two vectors P and Q is R If the magnitude of Q is doubled, the new resultant becomes perpendicular to P , then the magnitude of R is A) 2 P Q 2PQ B) 2 P Q 2PQ C) Q D) P Q Transcript Ex 102, 8 Find the unit vector in the direction of vector (𝑃𝑄) ⃗ , where P and Q are the points (1, 2, 3) and (4, 5, 6);
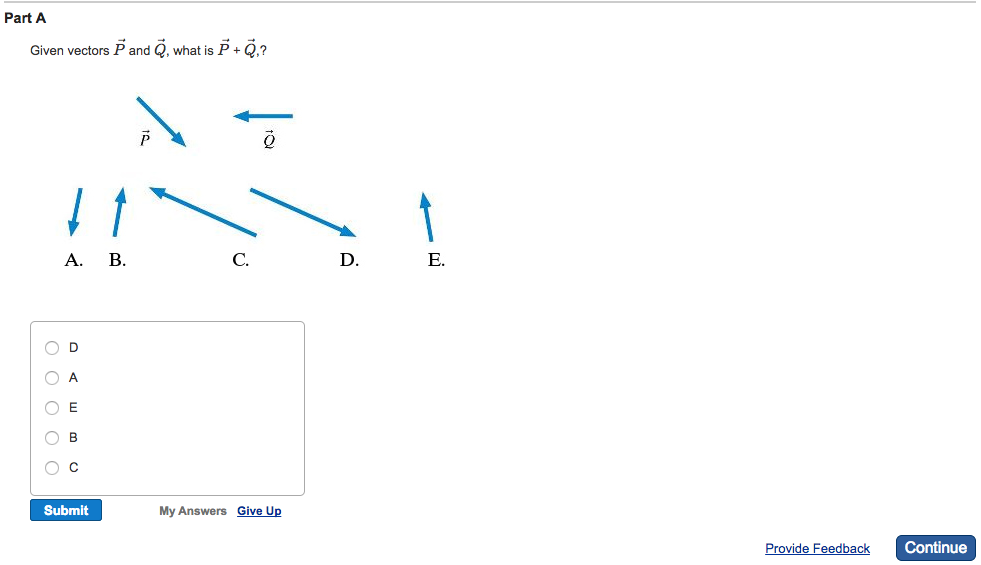



Part A Given Vectors P And Q What Is P 2 O A O B Chegg Com



What Is The Angle Between The Two Vectors P Q And P Q Quora
That is AB → =p, BC → =q ⇒ AC → =pq This definition of vector addition is referred to as the triangle law of addition You can then subtract vectors, for a−b simply means a−()b For example ABSolution Given, the position vectors of P and Q are respectively, a and b Taking, PR=5PQ R−P=5(Q−P) R=5Q−5PP R=5Q−4P R=5b−4a If vector P vector Q = vector P vector P then the angle between the vectors vector P and vector Q (a) 0° (b) 90°




If Vector P Vector Q P Q Then The Angle Between P And Q Is Maths Vector Algebra Meritnation Com
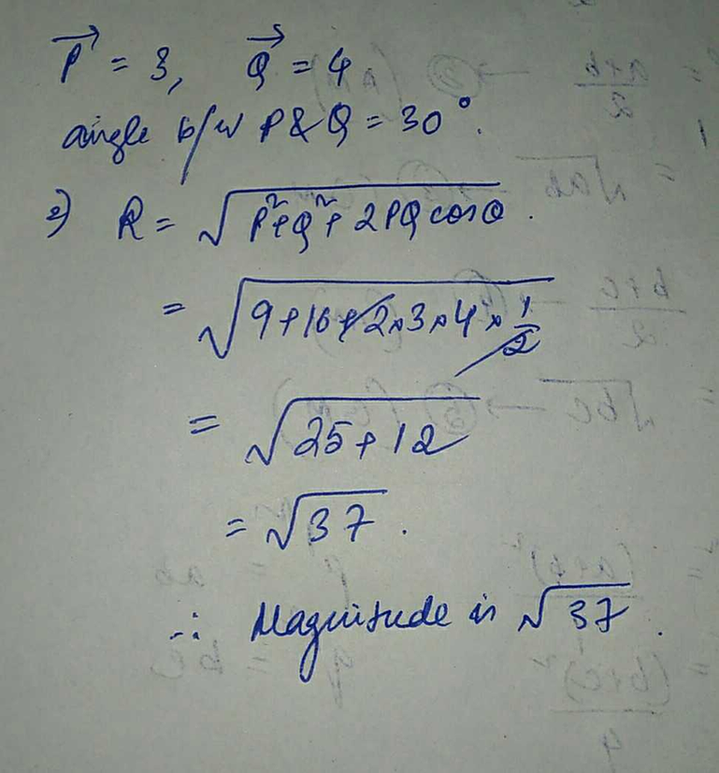



Two Vectors P And Q Have Magnitudes 3 Units And 4 Units Resp Scholr
If the roots of the equation bx 2 cx a = 0 be imaginary then for all real values of x, the expression 3b 2 x 2 6bcx 2c 2 is If the roots of the equation λ 2 8λ μ 2 6μ = 0 are real, then μ lies between If the scalar and vector products of two vectors A and B are equal in magnitude, then the angle between the two vectors is Explanation Given, → P → Q = → R So, we can write, ∣∣ ∣→ R ∣∣ ∣ = √P 2 Q2 2P Qcosθ ,where θ is the angle between the two vectors Or, R2 = P 2 Q2 2P Qcosθ Given, P 2 Q2 = R2 So, R2 = R2 2P Qcosθ Or, 2P Qcosθ = 0 So, cosθ = 0"P only if Q" (if P holds, then Q had better hold for the constraint to be satisfied);




The Resultant Of Two Vectors P And Q Is R If Q Is Doubled Then The New Resultant Vector Is Brainly In



If P Dot Q Vector 0 And P Q Vector 0 Then What Is The Angle Between The Q And R Vector Quora
If P is null, then P Q = P − Q gives Q = − Q , implying both are null, which is absurd Also if they are perpendicular, the direction of sum and difference of vectors will beIf the sides AB and BC of a triangle ABC represent the vectors p and q, then the third side, AC, is defined as the vector sum of p and q;31 If a dot product of two nonzero vectors is 0, then the two vectors must be what to each other?
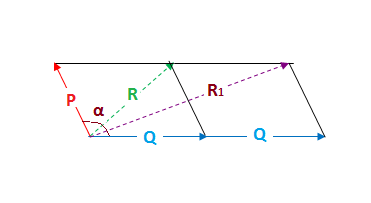



The Resultant Of Two Vectors P And Q Is R If Q Is Doubled Then The New Resultant Vector Is Perpendicular To P Then R Is Equal To Socratic




Find The Angle Between Two Vectors P Vector And Q Vector If Resultant Of The Vector Is Given By R 2 Brainly In
Find the angle between two vectors p and q, if p x q = pq Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, P dilip_k Let the angle between two vectors P and Q be α and their resultant is R So we can write R2 = P 2 Q2 2P Qcosα1 When Q is doubled then let the resultant vector be R1, So we can write R2 1 = P 2 4Q2 4P Qcosα2 Again by the given condition R1 is perpendicular to P So 4Q2 = P 2 R2 13P,Q,R,S are vector of equal magnitude If PQR=0 angle between p and Q is 0 If P =0 angle between 7 and S is 0, The ratio of e, to 0, is 1) 12 2)21 3) 11 4)1 13



Www Ualberta Ca Rjia Math214 Part2 Lec2a Pdf




If P Vector Dot Q Vector Is Equal To Pq Then Angle Between P And Q Is Brainly In
In triangle law head of vector P is connected to tail of vector Q But angle between two vectors is possible tail to tail Hence shift Vector Q from head of vector P to tail of vector P without changing direction and keeping the shift parallel This way we get the angle between vector P and Vector QThe PQ and PQ are its diagonals Unless you know the lengths of the sides, we cannot proceed Note that if P and Q have equal magnitudes, the parallelogram is a rhombus, in which case the angle between the diagonals is 90 Given that (P vector Q vector) = (P vector Q vector)




The Resultant R Of Vector P Andq Is Perpendicular To P And R P Both Then Angle Betwwen P And Q Is




If The Resultant Of Two Forces Of Magnitudes P And Q Acting At A Point At An Youtube




P Q R And P Q C Then Q Is P Q R Are Vectors




Direction A Or Pq Is A Vector P Is Initial Point Chegg Com




What Is The Angle Between P Q And P Q Youtube




2 Let P Q Be Points With Co Ordinates P 2 3 Chegg Com




Find The Unit Vector In The Direction Of Vector Pq Where P And Q Are




Given P Q R If Vector P Vector Q Vector R Then The Angle Between Vector P And Q Is Theeta1 If Vector Brainly In




Solved Let P Q Be Points With Co Ordinates P 2 3 Q 2 Chegg Com
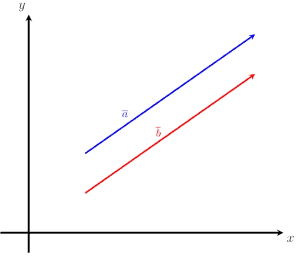



Equal Vectors Explanation Examples




If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora




5 Given Vectors A 3i 4 K And B 21 5k Find Chegg Com




Property 2 If P Q Is A Rational Number And M Is A Common Divisor Of P And Q Then P Q P M Q M




Example Using Vectors To Find The Angles Of A Triangle Youtube




If Vector P I J K And Q I 2j K Find A Vector Of Magnitude




If Vector P Q And R Have Magnitude 5 12 And 13 Units And Vec P Vec Q Vec R The Angle Between Q And R Is




Proposition 2 10 Let X E R Be Given Let 1 S Piq Soo Chegg Com




The Sum Of The Magnitudes Of Two Vectors P And Q Is 18 And The Magnitud Youtube




The Resultant Vec P And Vec Q Is Perpendicular To Vec P What Is The Angle Between Vec P And Vec Q



What Is The Angle Between The Two Vectors P Q And P Q Quora




Two Forces P And Q Have A Resultant Perpendicular To P The Angle Between The Forces Is Quora




The Resultant Of Two Forces P And Q Is Of Magnitude P If P Be Doubled The Resultant Will Be Inclined To Q At An Angle




If Vector P Q And R Have Magnitude 5 12 And 13 Units And Youtube




The Resultant Of Two Vectors P And Q Is R If Q Is Doubled The New R Askiitians




09uel 3 If P Q Then Which Of The Following Is Not Correct P Q An The Following Is Not Correct P Are Unit Vectors And P Q Are




If The Resultant Of Two Forces Of Magnitudes P And Q Acting A Point At An Angle Of 60 0is Sqrt7q Then P Q Is
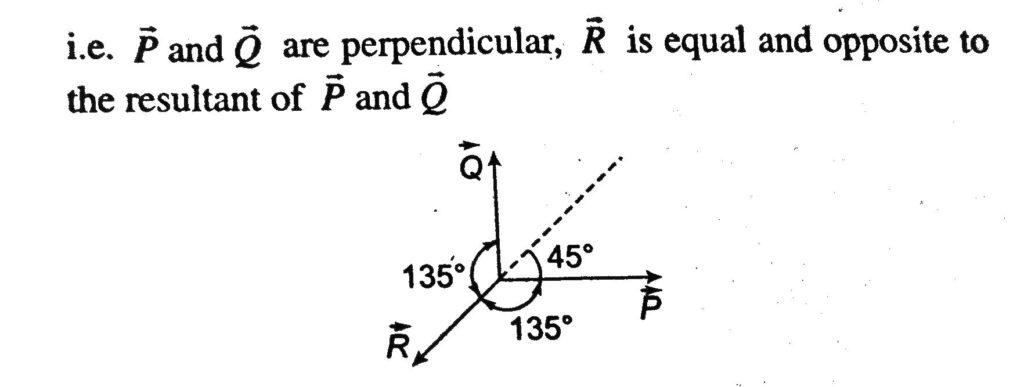



Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And




The Position Vectors Of P And Q Are Respectively A And B If R Is A Point On Pq Such That Pr 5pq Then The Position Vector Of R Is




If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora




If P 1 2 And Q 3 7 Are Two Points Express The Vectors Vec Pq In Terms Of Unit Vectors Hatiand Hatj Also Find The Distance Between Points P And Q What Is The Unit Vector




Given P Q R And That R Is Perpendicular To P If P R Then What Is The Angle Between P And Q Quora




Euclidean Distance Wikipedia
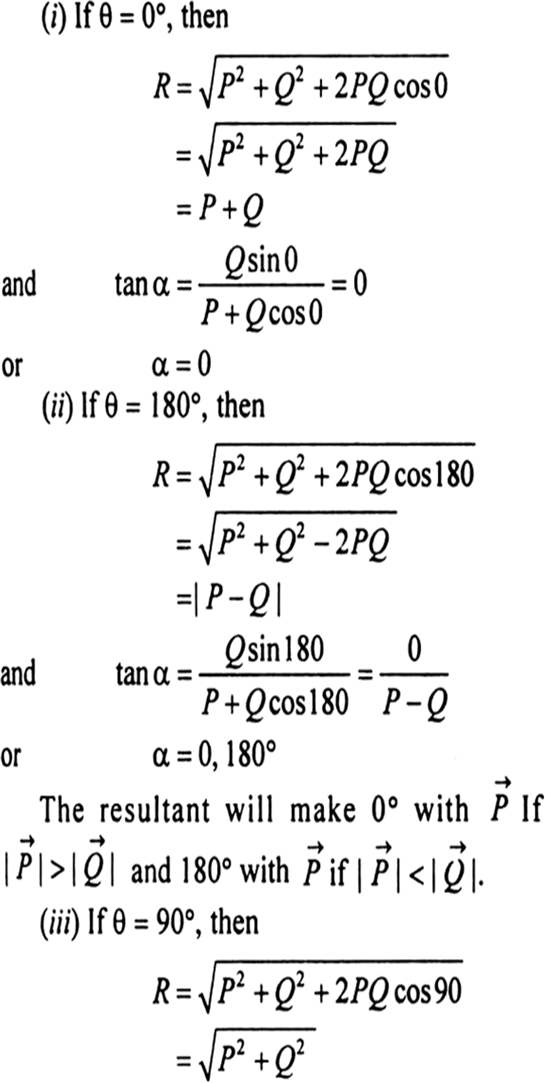



Find The Magnitude And Direction Of Resultant Of Two Vectors Analytically Discuss The Special Cases For Angle Between The Vectors I 0 Ii 180 Iii 90 From Physics Motion In A Plane Class 11 Cbse




Given P Q R If Vector P Vector Q Vector R Then The Angle Between Vector P And Q Is Theeta1 If Vector Brainly In



Search Q Angle Between Two Vectors Tbm Isch




The Angles Between P Q And P Q Will Be Youtube




The Resultant Of Two Vectors P And Q Is Perpendicular To P And Its Magnitude Is Half Of That Of Q Brainly In




9 At What Angle Do The Two Forces P Q And P Q Act So That The Resultant Is 3p Q Ans 60




If Vecp Vecq Pq Then Angle Between Vecp And Vecq Is




Find The Unit Vector In The Direction Of Vector Pq Where P And Q Are




The Resultant Of Two Vectors P And Q Is R If The Vector Q Is Reversed Then The Resultant Becomes S Then Choose The Correct Option




If P Q P Q And O Is The Angle Between P And Q Then A 0 00 B 0 900 C P 0
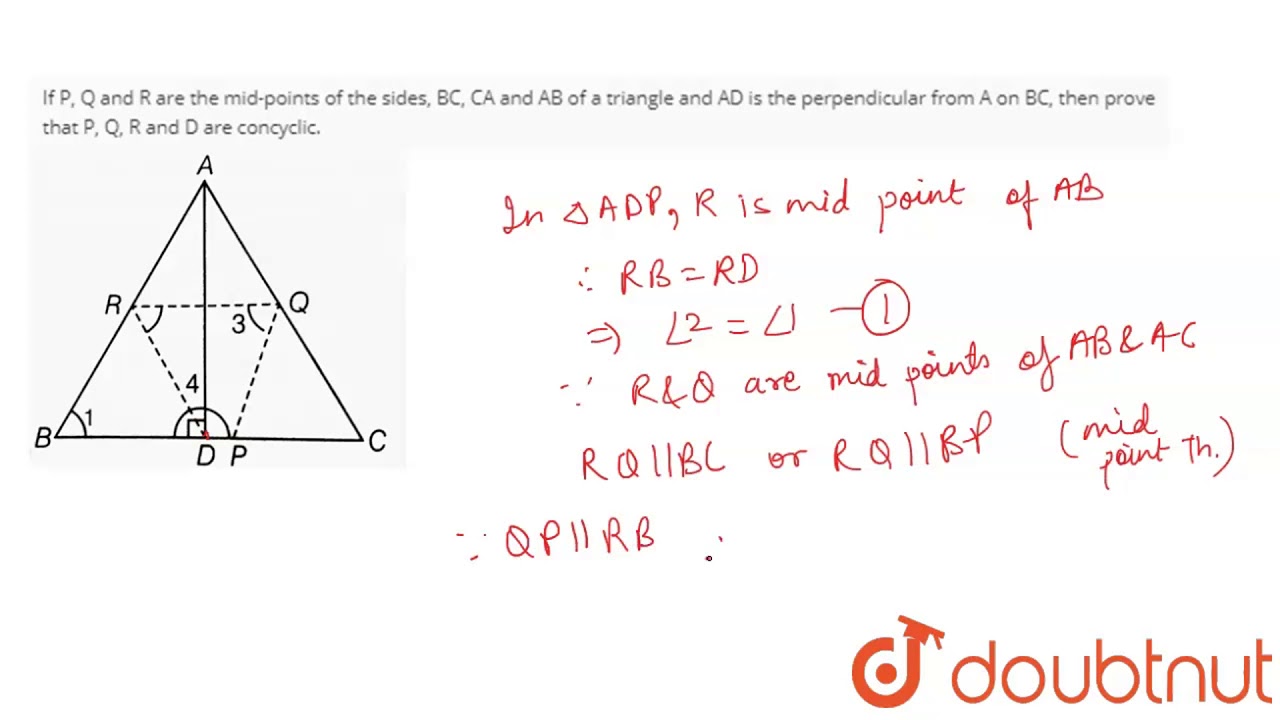



If P Q And R Are The Mid Points Of The Sides Ca And Ab Of A Triangle And Ad Is The Perpen Youtube




If P Q P Q What Is The Angle Between The P Vector And Q Vector Quora




Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube



The Resultant Of Two Forces P And Q Is R If Q Is Doubled The New Resultant Is Perpendicular To P How Can I Prove Q R Quora




Express The Vector With Initial Point P And Terminal Chegg Com



The Resultant Of The Vector P And Q Is Perpendicular To The Vector P What Is The Angle Between P And Q Quora




Three Vectors P Q And R Are Shown In The Figure Let S Be Any Point On The Vector R The Distance Between The Points P And S Is B R




Find Angle Between P Vector And Q Vector If Resultant Is Given By R 2 P 2 Q 2 Physics Topperlearning Com 40y2cnxx




Given That P Q R If P Q R Then The Angle Between P And R Is Theta1 If P Q R 0




If P Q P Q Then




Given P A B And Q A B If The Magnitude Of Vector P And Q Are Equalthen What Is The Angle Between Brainly In




09uel 3 If P Q Then Which Of The Following Is Not Correct P Q An The Following Is Not Correct P Are Unit Vectors And P Q Are




Given That P Q R If P Q R Then The Angle Between P And R Is Theta1 If P Q 0 Then The Angle Physics Physics And Mathematics Meritnation Com




Given That P Q R If Pvector Qvector Rvector Then The Angle Between Pvector And Rvector Is 81 If Pvector Qvector Rvector 0 The The Angle Between Pvector And Rvector Is What Is The Relation Between 81




If Vector P I J K And Q I 2j K Find A Vector Of Magnitude




If Angle Between 2 Vector P Vector And Q Vector Is 60 And Magnitude Of Resultant Of This Vector Is Brainly In




Negative Vectors Explanation Examples



Q Tbn And9gctsezf Wnftk3ffjh7za7g1uuuz0uvxp6tgviupbup 79nnvg L Usqp Cau




The Magnitude Of The Three Vectors P Q R Are Respectively 12 And 51 And 39 And If Vector P Vector Q Brainly In
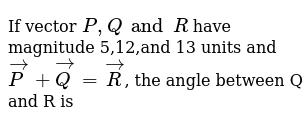



Angle Between Vector P Q P Q Wil Be




When Two Vectors Of Magnitudes P And Q Are Inclined At An Angle Theta The Magnitudes Of Their Resultant Is 2p When The Inclination Is Changed To 180 Theta The Magnitudes Of The




Find The Unit Vector In The Direction Of Pq Vector Where P And Q Are The Points 1 2 3 And 4 5 6 Youtube



Two Vectors P And Q Are Inclined Towards Each Other At An Angle Theta What Is The Unit Vector Perpendicular To The P Vector And The Q Vector Quora
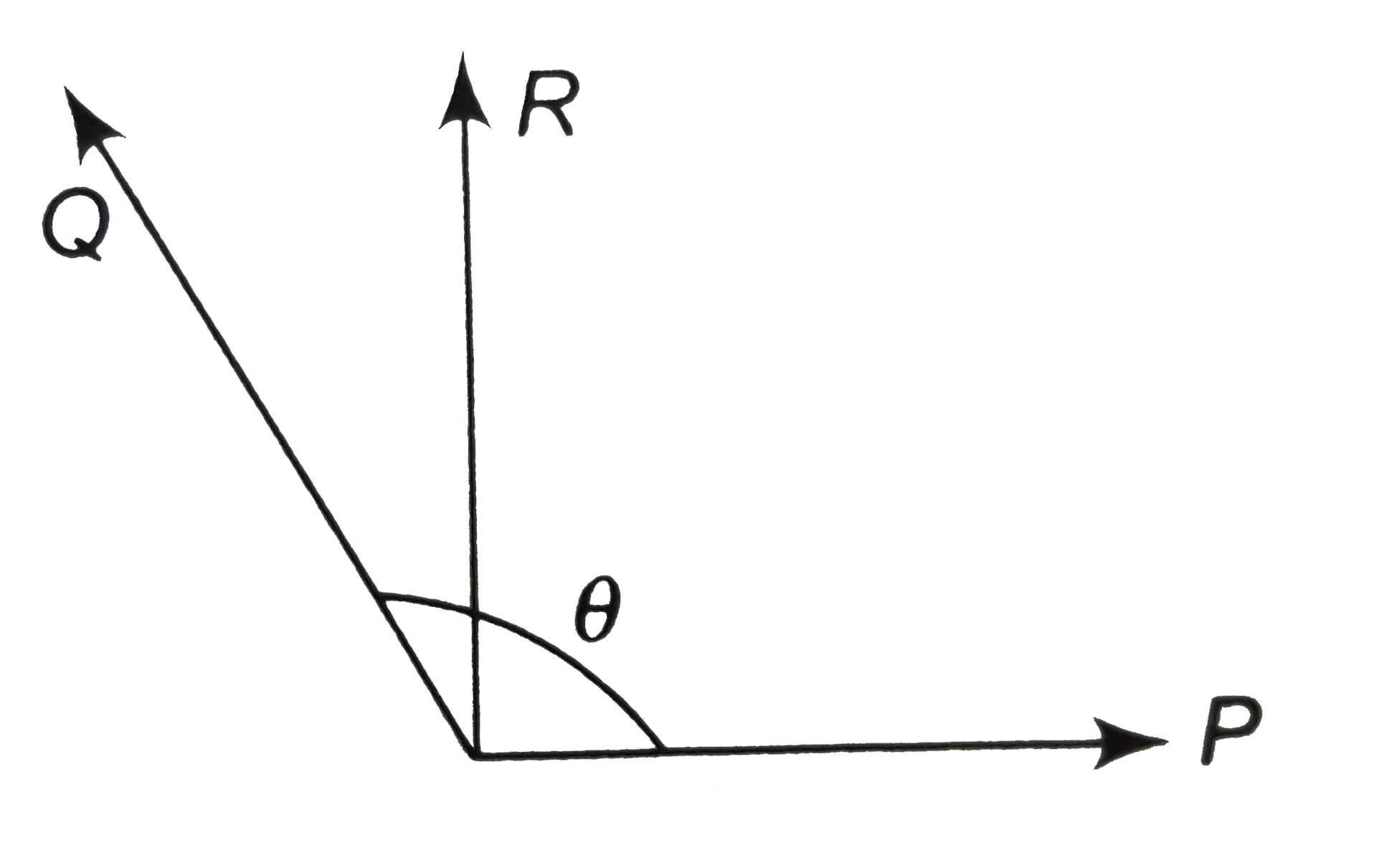



The Resultant Vec P And Vec Q Is Perpendicular To Vec P What Is The Angle Between Vec P And Vec Q




Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube




Two Forces P And Q Are In Ratio P Q 1 2 If Their Resultant Is At An Angle Tan 1 Sqrt3 2 Youtube




16 A 10 At What Angle The Two Vectors Of Magnitude P Q And P Q Should Act So That Their Resultant Is Vp2 0 1 Cos P2 02 L P2 02 V 2 Cos 1




At What Angle Two Forces P Q And P Q Act So That Resultant Is I Sqrt 2 P 2 Q 2 Youtube




At What Angle Two Forces P Q And P Q Act So That Resultant Is I Sqrt 2 P 2 Q 2 Ii Sqrt 2 P 2 Q 2 Iii Sqrt 2 P 2 Q 2



What Is The Angle Between P And The Cross Product Of P Q And P Q Quora




If P Q R And P Q Sqrt 3 And R 3 Then The Angle Between P And Q Is




The Resultant R Of Vectors P And Q Is Perpendicular To P Also P R The Angle Between P And Q Is



E2ynfmgjhhpbam



How To Prove That Non Zero Vectors P Q P Q If They Re Perpendicular Quora
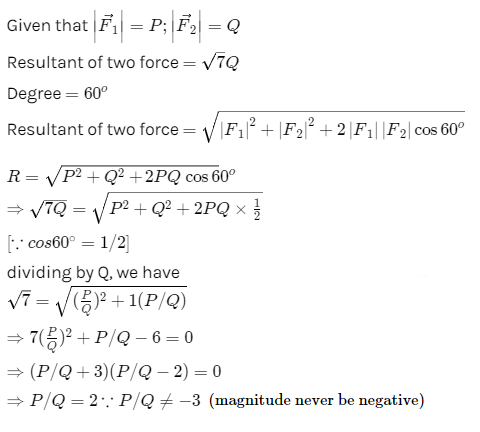



If The Resultant Of Two Forces Of Magnitudes P And Q Acting At A Poin Askiitians




If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora




At What Angle Do The Forces P Q And P Q Act So That Their Resultant Is Under Root 3p Square Q Square Brainly In




If 8 0 And Two Vectors P And Q Are Parallel To Each Other Then P Q Pq Brainly In



Q Tbn And9gcqg4xfxnj8 Jib5v6vrqkauybff541lt8 Nw9skbmychmoro Ip Usqp Cau




How To Prove That Non Zero Vectors P Q P Q If They Re Perpendicular Quora


